Класифікація паралелограмів

                                      Чотирикутники. Основні елементи чотирикутника.

Означення. Чотирикутником називається фігура, яка складається з чотирьох точок (вершин) на площині і чотирьох відрізків без самоперетинів (сторін), які послідовно з'єднують ці чотири точки. Таким чином, у чотирикутника  дві не сусідні сторони не перетинаються і чотири вершини не являються вершинами просторової фігури піраміди.

Означення. Дані чотири точки А, В, С і D – його вершини чотирикутника,  а чотири відрізки АВ, ВС, СD, DА – сторони чотирикутника.

Домовимося відрізки в чотирикутнику позначати так само, як і їх довжини;  АВ, ВС, СD, DА або  а, b, с, d.

Приклад. Нехай дано чотири точки А, В, С і D, кожні три із яких не лежать на одній прямій. Якщо їх сполучити послідовно відрізками, що не перетинаються, утвориться  чотирикутник АВСD (мал.1).

Означення. Дві вершини чотирикутника, які є кінцями однієї сто­рони чотирикутника, називаються сусідніми вершинами чотирикутника.

Приклад. Вершини В і С – сусідні вершини чотирикутника, бо є кінцями однієї сто­рони чотирикутника.

Означення. Дві сторони чотирикутника, які не мають спільних точок, називаються протилежні сторони.

Приклад. Дві сторони  АВ, СD –  протилежні сторони чотирикутника, бо не мають спільних точок.

Означення. Дві сторони, які мають спільну вершину, називаються сусідні сторони.

Приклад. Дві сторони  АD, СD –  сусідні сторони чотирикутника, бо мають спільну вершину.

Означення. Діагоналлю чотирикутника називається відрізок, який  з'єднує дві його несусідні вершини.

Приклад. Відрізки АС і ВD – це діагоналі чотирикутника АВСD, бо  кожний з цих відрізків з'єднує дві несусідні вершини чотирикутника.

Домовимося діагоналі в чотирикутнику позначати так само, як і їх довжини:  АС, BD або e, f  – діагоналі чотирикутника і їх довжини.

Кожний чотирикутник поділяє площину, якій він належить, на дві області.

Означення. Внутрішня область  чотирикутника – це множина усіх точок, які  знаходяться всередині чотирикутника, тобто обмежені сторонами чотирикутника.

Приклад. На малюнку 2 заштрихована внутрішня область чотирикутника, тобто це множина усіх точок, які  знаходяться всередині чотирикутника.

Означення. Зовнішня область – це множина усіх точок, які  знаходяться за межами чотирикутника, тобто необмежені сторонами чотирикутника.

Приклад. На малюнку 2 незаштрихована зовнішня область чотирикутника, тобто це множина усіх точок, які  знаходяться за межами чотирикутника.

Запам’ятайте: Об'єднання чотирикутника і його внутрішньої області називають також чотирикутником.

Саме такі чотирикутники мають на увазі, коли гово­рять про площі чотирикутників. Якщо не зрозуміло, про які чотирикутники йдеться,  тоді їх розрізняють: «чотирикут­ник як контур» і «чотирикутник як частина площини».

Означення. Внутрішніми кутами чотирикутника АВСD називають кути, що утворені сусідніми сторонами,  тобто, обмежують внутрішню область чотирикутника.   Позначають кути чотирикутника: ÐDАВ, ÐАВС, ÐВСD і ÐСDА, або коротко внутрішні кути позначають ще так:   ÐА = α, Ð В = b, ÐС = g, ÐD  = d,  – це величини(градуси, радіани) внутрішніх кутів чотирикутника.

Означення. Внутрішні кути чотирикутника називають проти­лежними  кутами чи сусідніми кутами залежно під того, протилежні чи сусідні їх вершини.

Запам’ятайте: Один з кутів чотирикутника може бути більшим від розгорнутого, тобто більшим від 180⁰.

Приклад. На малюнку 3 зображено чотирикутник з внутрішнім  кутом більшим від розгорнутого, тобто більшим від 180⁰.

Класифікація чотирикутників за найбільшим кутом.

На початку звертаємо вашу увагу на той факт, що існують не рівні чотирикутники  з усіма рівними сторонами.

Означення. Чотирикутник з кутом більшим від розгорнутого, тобто більшим, ніж 180⁰,  називають неопуклим чотирикутником. (мал. 3).

Означення. Якщо один із кутів чотирикутника дорівнює 180°, та­кий чотирикутник називають виродженим.

Означення. Якщо кожний кут чотирикутника менший від роз­горнутого, його називають опуклим чотирикутником. (мал. 2 або мал. 4.).  

Ми не роз­глядатимемо вироджені чотирикутники і, пишучи «чотирикутник», матимемо на увазі, що він невироджений.

Ознака опуклого чотирикутника: Для того щоб чотирикутник був опуклим, необхідно і достатньо, щоб його діагоналі перетинались.

Отже, діагоналі опуклого чотирикутника перетинаються і обидві лежать у його внутрішній області.

Діагоналі неопуклого чотирикутника не перетинаються і тільки одна з них лежить у внутрішній області чотирикутника.

Властивість опуклого чотирикутника: Опуклий чотирикутник лежить по один бік від будь-якої прямої, яка містить його сто­рону

Означення. Суму довжин усіх сторін чотирикутника Р = АВ + ВС + СD + DА називають перимет­ром.  Половину периметра чотирикутника Р/2 = p  називають  півпериметром чотирикутника.

Домовимося відрізки в чотирикутнику позначати так само, як і їх довжини. Дотримуватимемось здебільшого таких позначень (мал. 4):

АВСD – чотирикутник;

А, В, С, D – вершини чотирикутника;

АВ, ВС, СD, DА або а, b, с, d – сторони і їх довжини чотирикутника;

ÐDАВ, ÐАВС, ÐВСD і ÐСDА  або ÐА = α, Ð В = b, ÐС = g, ÐD  = d,  – внутрішні кути чотирикутника;

АС, BD або e, f  – діагоналі чотирикутника і їх довжини; Ð j – кут між діагоналями чотирикутника.

К, L, М, N – середини сторін чотирикутника;

Е, F  – середини діагоналей чотирикутника;

p = Р/2 = (АВ + ВС + СD + DА):2 – півпериметр  чотирикутника.

Означення. Правильним  чотирикутником називається чотирикутник, всі сторони і всі кути якого рівні.

Означення. Правильний чотирикутник називається квадратом.

Приклад. Чотирикутник, у якого всі кути прямі, тобто рівні 90⁰, дві діагоналі рівні  і чотири сторони рівні  є квадратом. Чотирикутник, у якого рівні дві діагоналі  і кути  між діагоналями прямі, тобто рівні 90⁰ є квадратом. (Мал. 5)

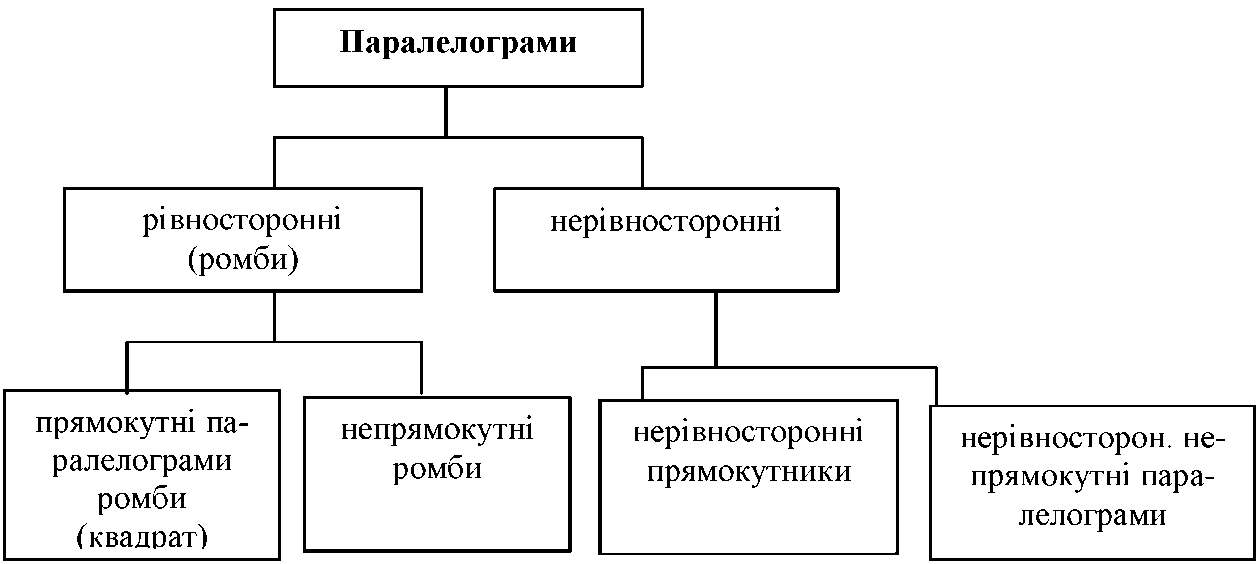
Класифікація чотирикутників за кількістю пар паралельних сторін.

Паралелограм.

 Кожний чотирикутник можна розглядати як спільну частину (переріз) двох смуг, смуги і кута або двох кутів.

У першому випадку маємо парале­лограм.

Означення. Чотирикутник називається паралелограмом, якщо кожна пара протилежних сторін чотирикутника лежать на паралельних прямих.

Означення . Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні, тобто, пара протилежних сторін чотирикутника лежать на паралельних прямих.

Означення. Чотирикутник називається вільним, якщо у нього жодна пара протилежних сторін чотирикутника не лежить на паралельних прямих.

Приклад. Паралелограм  АВСD – це чотирикутник, у якого протилежні сторони паралельні, тобто лежать на паралельних прямих (мал. 6).

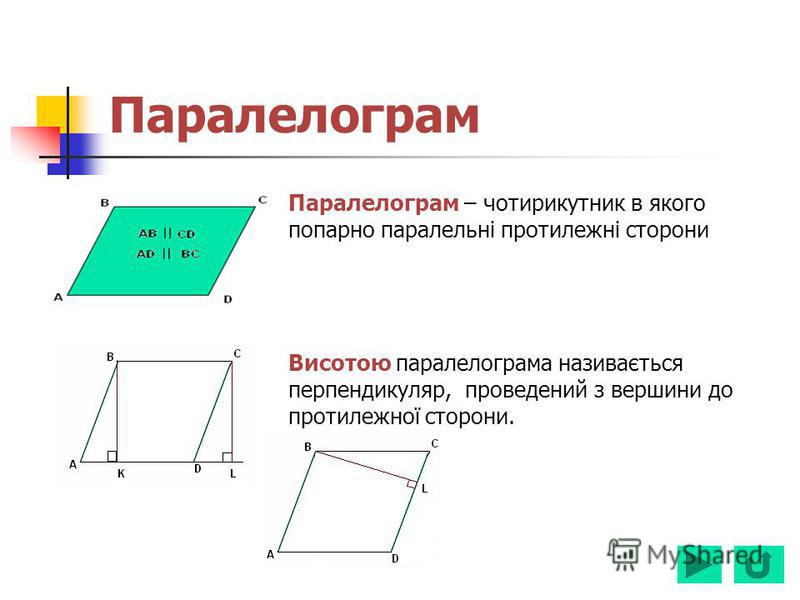
Означення. Висота паралелограма – це відрізок, що перпендикулярний до протилежних сторін паралелограма. У паралелограма з вершини тупого кута можна провести дві висоти, кут між якими дорівнює гострому куту паралелограма.

Паралелограм має центр симетрії – це точка перетину діагоналей.

Властивості паралелограма.

Теорема 1. Протилежні сторони паралелограма рівні (|AB| = |CD|, |AD| = |BC|).

Теорема 2. Протилежні кути паралелограма рівні (ÐA = ÐC, ÐB = ÐD).

Доведення. Нехай АВСD – даний паралелограм (мал. 6)..  Проведемо діагоналі паралелограма АС, BD. Нехай О – точка їх перетину. Рівність протилежних сторін АВ і СD випливає з рівності трикутників АОВ і СОD. У них кути при вершині О рівні як вертикальні, а ОА + ОС і ОВ + OD. Так само з рівності трикутників АОD і СОВ випливає рівність другої пари протилежних сторін АD і ВС.

Рівність протилежних ÐАВС і ÐСDА випливає з рівності трикутників АВС і СDА (за трьома сторонами). У них АB=СD і ВС = DА за доведеним, а сторона АС спільна.

Так само рівність протилежних кутів ÐВСD і ÐDАВ випливає з рівності трикутників ВСD і DАВ. Теорему доведено.

Теорема 3. Діагоналі паралелограма перетинаються і точкою перетину діляться навпіл (|AO| = |OC|, |BO| = |OD|).

Теорема 4. Сума кутів, прилеглих до однієї сторони, рівна 180°.

Теорема 5. Сума квадратів діагоналей паралелограма рівна сумі квадратів його чотирьох сторін

Теорема 6. Якщо діагоналі чотирикутника перетинаються і в точці перетину діляться пополам, то цей чотирикутник – паралелограм.

Ознаки паралелограма.

Чотирикутник ABCD є паралелограмом, якщо виконується одна з наступних умов:

Ознака 1. Протилежні сторони попарно рівні (|AB| = |CD|, |AD| = |BC|).

Ознака 2. Протилежні кути попарно рівні.

Ознака 3. Дві протилежні сторони рівні і паралельні (|AB| = |CD|, AB || CD).

Ознака 4. Діагоналі діляться в точці їх перетину навпіл (|AЕ| = |ЕC|, |BЕ| = |ЕD|).

Доведення ознак.  Нехай чотирикутник ABCD такий що: |AB| = |CD| і |BC| = |AD|.

Проведемо діагональ BD, ми отримаємо два трикутники, які рівні, оскільки діагональ BD - спільна сторона для двох трикутників. |AB| = |CD| і |BC| = |AD| (з умови). З рівності цих трикутників виходить: ÐABD = ÐBDC і ÐABD = ÐCBD і внаслідок цього AB||CD і BC||AD.

Нехай чотирикутник ABCD такий що: BC || AD і |BC| = |AD|.  Трикутники ABC і BCD рівні (дивись попередній доказ) => ÐBAC = ÐACD. Таким чином AB||CD.

Площу паралелограма можна знайти:

·        як добуток висоти на сторону, до якої проведена висота.

·        як добуток двох сторін і синуса кута між ними.

·        як половина добутку двох діагоналей і синуса кута між ними.

До паралелограмів належать відомі вам чотирикутники: прямокутник, ромб, квадрат.

Ромб

Означення. Ромб  – це чотирикутник, у якого всі сторони рівні.

Означення. Ромб, у якого прямі  кути, називається  квадратом.

Слово «ромб» вперше уживається у працях Герона і Паппа Александрійського.

Елементи симетрії ромба.

Ромб має наступні елементи симетрії: одну вісь симетрії яка перпендикулярна площині ромба і проходить через його центр;  дві осі симетрії другого порядку, з яких дві проходять вздовж діагоналей ромба.

Властивості ромба

Теорема 1. Ромб є параллелограммом. Його сторони, що протилежать, попарно паралельні, АВ || CD, AD || ВС.

Теорема 2. Діагоналі ромба перетинаються під прямим кутом (AC ^ BD) і в точці перетину діляться навпіл.

Теорема 3. Діагоналі ромба є бісектрисами його кутів (ÐDCA = ÐBCA, ÐABD = ÐCBD і т.  д.).

Теорема 4. Сума квадратів діагоналей рівна квадрату сторони, помноженому на чотири.

Площа ромба

Площа ромба рівна половині добутку його діагоналей. Оскільки ромб є параллегограммом, тоді його площа також рівна добутку його сторони на висоту.
Площа ромба рівна квадрату його сторони на синус кута між сторонами.

Прямокутник

Означення. Прямокутник – це чотирикутник, у якого всі  кути прямі, тобто, рівні 90°.

Означення. Довжиною прямокутника називають довжину довшої пари його сторін, а шириною  довжину коротшої пари сторін.

Властивості  прямокутника.

Теорема 1. Діагоналі прямокутника рівні.

Теорема 2. Прямокутник є паралелограмом  його протилежні сторони паралельні.

Теорема 3. Сторони прямокутника є одночасно його висотами.

Теорема 3. Квадрат діагоналі прямокутника рівний сумі квадратів двох його суміжних сторін.

Теорема 4. Прямокутник, який одночасно є і ромбом (у якого всі сторони рівні) – це квадрат.

Теорема 5. Довжина діагоналі прямокутника обчислюється за теоремою Піфагора і рівна квадратному кореню з суми квадратів довжини і ширини.

Площа і периметр

Величина площі прямокутника рівна твору ширини прямокутника на його висоту.

Периметр прямокутника рівний подвоєній сумі довжин його ширини і висоти.

квадрат  один з окремих випадків прямокутника.

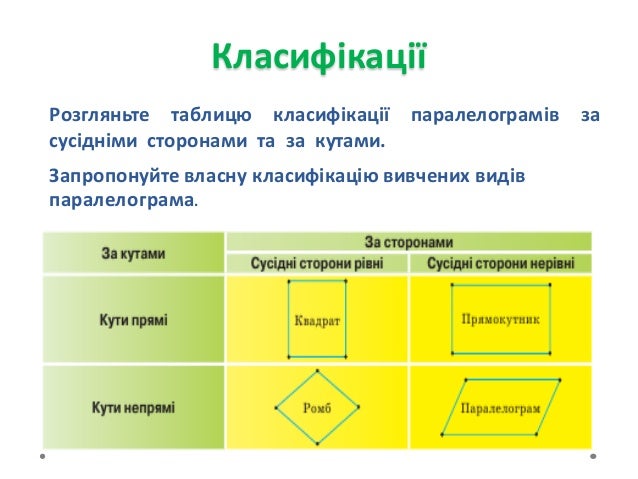
Квадрат

Означення. Квадрат – правильний чотирикутник.  Може бути визначений, як прямокутник, у якого дві сусідні сторони рівні або як ромб у якого всі кути прямі.

Елементи симетрії

Квадрат має наступні елементи симетрії: одну вісь симетрії яка перпендикулярна площині квадрата і проходить через його центр;  чотири осі симетрії другого порядку, з яких дві проходять вздовж діагоналей квадрата, а інші дві – паралельно сторонам, і проходять через середини сторін квадрата.

Квадрат володіє найбільшою кількістю симетрій серед всіх чотирикутників.

Властивості квадрата:

Теорема 1. При розрізанні  квадрата діагоналлю отримуємо два рівнобедрених прямокутних трикутники.

Теорема 2. Діагональ квадрата рівна добутку сторони і квадратного кореня з двійки.

Теорема 3. Радіус описаного кола дорівнює половині добутку сторони і квадратного кореня з двійки.

Теорема 3. Радіус вписаного кола дорівнює половині сторони квадрата.

Теорема 4. У квадрата центри вписаного і описаного кіл  і центр симетрії співпадають.

Периметр і площа квадрата

Нехай a – сторона квадрата, R – радіус описаного кола, r – радіус вписаного кола. Тоді периметр квадрата рівний: P = 4a  = 4(2^0,5)R² = r². 

а площа S квадрата розраховується по формулі

S = а² = 2R² = 4r². 

Візуальні  завдання з теми "Паралелограми"