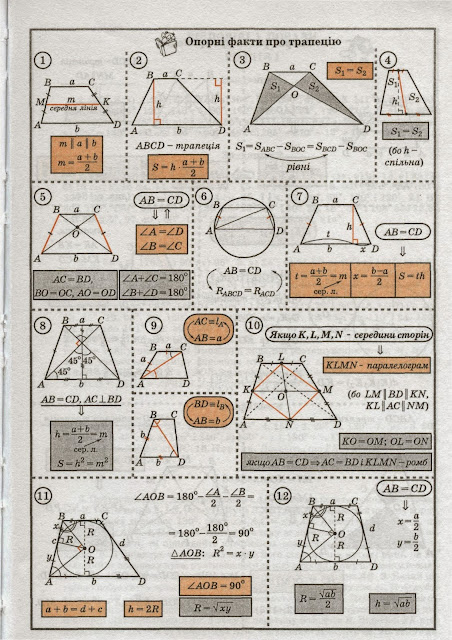
Властивості трапеції

"Найбільша помилка - вважати, що ти ніколи не помиляєшся."

Томас Карлейль

Трапеція

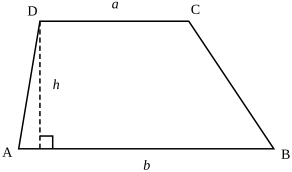
Трапе́ція — це чотирикутник, дві протилежні сторони якого паралельні. Паралельні сторони називаються основами трапеції (сторони AB та DC на малюнку). Інші сторони називаються бічними сторонами (сторони AD та CB).

Виділяють три спеціальні класи трапецій:

· Рівнобічна трапеція, тобто трапеція у якої бічні сторони рівні.

· Прямокутна трапеція — це трапеція у якої два кута прямі.

· Різностороння трапеція, у якої всі сторони різні.

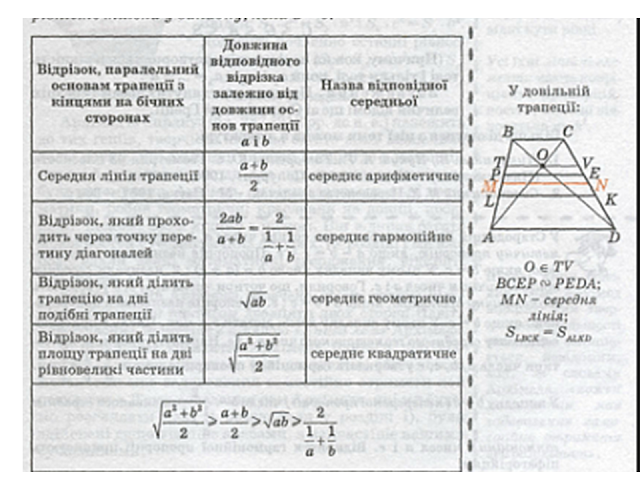
Відрізок, який сполучає середини бічних сторін, називається середньою лінією трапеції.

Середня лінія паралельна основам трапеції, а її довжина дорівнює їх півсумі:

http://spn1967.blogspot.com/2014/12/blog-post.html
Ð ÐµÐ·ÑƒÐ»ÑŒÑ‚Ð°Ñ‚ Ð¿Ð¾ÑˆÑƒÐºÑƒ Ð·Ð¾Ð±Ñ€Ð°Ð¶ÐµÐ½ÑŒ Ð·Ð° Ð·Ð°Ð¿Ð¸Ñ‚Ð¾Ð¼ "Ñ‚Ñ€Ð°Ð¿ÐµÑ†Ñ–Ñ"

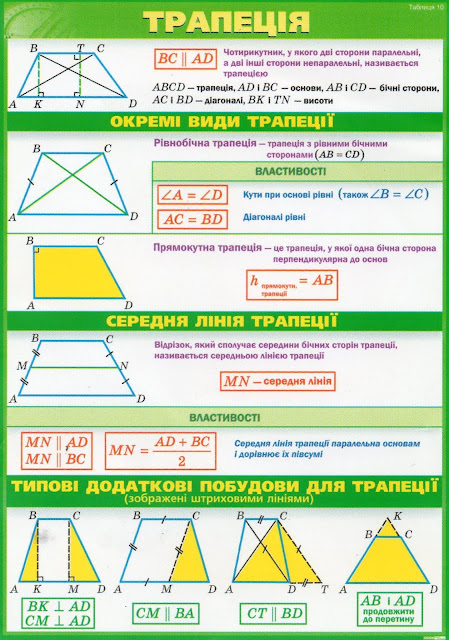
Основні види трапецій

Трапецію називають прямокутною, якщо у неї два суміжних кути дорівнюють 90°.

Гострою називається трапеція у якої кути, прилеглі до більшої основи гострі (менше 90°).

Трапецію називають рівнобічною, якщо її бічні сторони та кути, прилеглі до більшої основи, рівні. Ця трапеція має осьову симетрію.

Тупою називається трапеція, у якої один із кутів, прилеглих до більшої основи, тупий (більше 90°).

Трапеція з двома парами паралельних сторін називається паралелограмом. Паралелограм має дві осьові симметрії.

У широкому сенсі, всі паралелограми (включаючи ромби, прямокутники і квадрати) є трапеції. Прямокутники мають дзеркальну симетрію по середині ребер; ромби мають дзеркальну симетрію на вершинах, а квадрати мають дзеркальну симетрію з обох середніх ребер і вершин.

Дотичною називається трапеція, в яку має вписане коло.

Властивості

Для будь-якого опуклого чотирикутника такі властивості еквівалентні, і кожна передбачає, що чотирикутник є трапецією:

· Сума двох суміжних кутів дорівнює 180 градусів.

· Кут між однією основою і діагоналлю дорівнює куту між іншою основою та тією ж діагоналлю (внутрішні різносторонні кути рівні).

· Середня лінія трапеції паралельна основам і дорівнює їх півсумі.

· В трапецію можна вписати коло, якщо сума основ трапеції дорівнює сумі її бічних сторін.

· Точка перетину діагоналей трапеції, точка перетину продовжень її бічних сторін та середини основ лежать на одній прямій.

· Трикутники, утворені відрізками діагоналей та основами трапеції, подібні.

· Трикутники, утворені відрізками діагоналей та бічними сторонами трапеції, мають однакову площу.

· Відрізок, що з'єднує середини діагоналей, дорівнює піврізниці основ і лежить на середній лінії.

· Бісектриса будь-якого кута трапеції відтинає на її основі (або продовженні) відрізок, рівний бічній стороні.

· Якщо сума кутів при будь-якій основі трапеції дорівнює 90°, то відрізок, що з'єднує середини основ, дорівнює їх піврізниці.

· Якщо сума основ трапеції дорівнює сумі її бічних сторін, то в таку трапецію можна вписати коло, і навпаки.

· Будь-яку трапецію можна побудувати за довжинами чотирьох сторін.

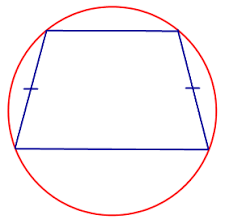
· В рівнобічній трапеції кути при основі, а також діагоналі рівні.

· Навколо рівнобічної трапеції можна описати коло.

Висота трапеції

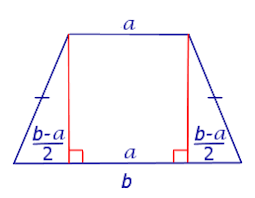
Висота — перпендикулярна відстань між основами. У разі, коли дві основи мають різну довжину (а ≠ b), висота трапеції може бути визначена через довжини чотирьох сторін за формулою:

, $h={\frac {\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2|b-a|}}$

де a, b — основи трапеції, а c і d — бокові сторони. Формула висоти трапеції, виражена через бокові сторони та кути, що прилеглі до більшої основи:

$h=c\cdot \sin \alpha =d\cdot \sin \beta$

Формула висоти трапеції, виражена через діагоналі та кути між ними:

. $h={\frac {d_{1}\cdot d_{2}}{a+b}}\cdot \sin \alpha ={\frac {d_{1}\cdot d_{2}}{a+b}}\cdot \sin \beta$

Формула висоти трапеції, виражена через площу:

$h={\frac {2S}{a+b}}={\frac {S}{m}}$ , де S — площа трапеції, m — середня лінія.

Банк задач з теми «Трапеція»

Довести наступні властивості трапеції.

1. Два внутрішні трикутники у трапеції, що обмежені частинами діагоналей трапеції та двома бічними сторонами трапеції мають рівні площі і хоча б один рівний кут.

2. Висота трапеції, що проведена через точку перетину діагоналей трапеції, ділиться у відношенні, яке дорівнює відношенню основ трапеції.

3. Діагональ трапеції утворює з основами рівні кути.

4. Два внутрішні трикутники, що обмежені частинами діагоналей трапеції та двома основами трапеції мають рівні кути(вони подібні, з коефіцієнтом подібності, що дорівнює відношенню довжин основ).

5. Середня лінія трапеції, що проведена між бічними лініями паралельна основам і дорівнює півсумі основ та не проходить через точку перетину діагоналей трапеції.

6. Відрізок, кінці якого лежать на двох основах трапеції, ділиться навпіл середньою лінією, що проведена між бічними сторонами трапеції.

7. Відрізок, кінці якого це середини основ трапеції, проходить і через точку перетину діагоналей трапеції.

8. Якщо відрізок паралельний основам трапеції з довжинами a, b, і ділить бічну сторона у відношенні m:n(рахуючи з верхньої основи), тоді довжина цього відрізка дорівнює (an+bm)/(n+m).

9. Якщо прямокутна трапеція має меншу діагональ, що перпендикулярна до більшої бічної сторони, тоді меша діагональ трапеції розрізає її на два подібних трикутники, з коефіцієнтом, що дорівнює відношенню бічних сторін прямокутної трапеції.

10. В трапецію можна вписати коло, якщо дві суми довжин протилежних сторін трапеції рівні між собою. Центр цього кола лежить в точці перетину бісектрис чотирьох внутрішніх кутів трапеції. Чотири точки дотику трапеції і вписаного кола утворюють чотирикутник з двома протилежними прямими кутами.

11. Навколо будь-якої рівнобічної трапеції можна описати коло. Центр цього кола лежить в точці перетину серединних перпендикулярів до усіх сторін трапеції.

12. Не завжди в рівнобічну, в прямокутну трапецію можна вписати коло.

13. Навколо прямокутної трапеції не можна описати коло.

14. Бічні сторони рівнобічної трапеції утворюють з основами рівні кути. Рівнобічна трапеція має рівні діагоналі. Якщо рівнобічна трапеція має перпендикулярні діагоналі, то висота трапеції дорівнює середній ліній трапеції( дві середні лінії трапеції рівні між собою).

15. Будь-яку трапецію можна відновити за довжинами чотирьох сторін..

16. Площа трапеції дорівнює добутку середньої лінії на висоту трапеції.

17. Прямокутна трапеція з гострим кутом, що дорівнює третині розгорнутого кута, та рівними між собою більшою бічною стороною та більшою основою трапеції має площу, яка дорівнює 0,75а²(3)^0,5 кв. од. , де а – більша бічна сторона. У такої прямокутної трапеції дві основи відносяться, як 1:2. У таку прямокутну трапецію не можна вписати коло.

18. Прямокутна трапеція має площу, що дорівнює добутку середньої лінії на меншу бічну сторону трапеції.

19. Якщо в прямокутну трапецію можна вписати коло, то радіус вписаного кола дорівнює середньому геометричному двох відрізків, на які розбиває точка дотику більшу бічну сторону.

20. Кути при бічній стороні трапеції дорівнюють 180^о.

Ознаки рівнобічної трапеції

Ознака 1. Якщо у трапеції кути при основі рівні, то трапеція рівнобічна.

Ознака 2. Якщо у трапеції діагоналі рівні, то трапеція рівнобічна.

Ознака 3. Якщо у трапеції діагоналі утворюють з основами рівні кути, то трапеція рівнобічна.

Якщо середини чотирьох сторін рівнобічної трапеції послідовно з’єднати відрізками, то одержимо ромб. Кути цього ромба дорівнюють кутам між діагоналями трапеції.

Якщо середини чотирьох сторін рівнобічної трапеції з перпендикулярними діагоналями послідовно з’єднати відрізками, то одержимо квадрат. У рівнобічній трапеції з перпендикулярними діагоналями висота дорівнює середній лінії.

Якщо менша та більша основи трапеції рівні відповідно a та b, тоді наступний перелік відрізків, що паралельні основам трапеції і мають таку довжину, що записані у порядку зростання:

2ab(a + b)^-1– проходить через точку перетину діагоналей трапеції (це середнє гармонійне основ).

(ab)^0,5– ділить трапецію на дві подібні трапеції (це середнє геометричне основ).

0,5(a + b) – ділить будь-яку бічну сторону у відношенні 1:1 (це середнє арифметичне основ).

0,5(a²+ b²)^0,5– ділить дану трапецію на дві рівновеликі трапеції (це середнє квадратичне основ).

а < 2ab(a + b)^-1< (ab)^0,5< 0,5(a + b) < 0,5(a²+ b²)^0,5< b

Якщо менша та більша основи трапеції рівні відповідно a та b, тоді відрізок, що паралельний основам трапеції і має довжину (an+ bm)(n + m)^-1 ділить бічні сторони у відношенні n:m.

Коло можна описати навколо довільної рівнобічної трапеції і не можна описати навколо довільної прямокутної та різнобічної трапецій.

Центр кола, що вписаний в трапецію лежить в точці перетину бісектрис внутрішніх кутів трапеції.

Із центру вписаного в трапецію кола будь-яку бічну сторону видно під прямим кутом, а радіус вписаного кола дорівнює
(nm)^0,5, де точка дотику кола ділить бічну сторону на відрізки n од.довж та m од.довж.

Описана трапеція може бути прямокутною, рівнобічною, різнобічною, і у неї сума основ дорівнює сумі бічних сторін.

Середня лінія описаної трапеції дорівнює півсумі бічних сторін.

Якщо діагоналі рівнобічної трапеції перпендикулярні, то вона не являється описаною.

Діагоналі трапеції розрізають трапецію на чотири трикутники, серед яких два трикутники є подібними (вони прилягають до основ трапеції) і два трикутники є рівновеликими, (вони прилягають до бічних сторін трапеції), площа рівновеликих трикутників дорівнює середньому геометричному площ двох подібних трикутників, прилягають до основ трапеції

S=(S₁S₂)^0,5.

Банк задач з теми «Трапеція»

Задачі на трапеціях

1. Основи трапеції 10 см і 15 см, а діагоналі — 7 см і 24 см. Знайдіть висоту трапеції.

2. Діагоналі рівнобічної трапеції діляться точкою перетину у відношенні 1 :4. Знайдіть периметр трапеції, якщо його бічна сторона і висота дорівнюють відповідно 20 см і 16 см.

3. Два кути трапеції при одній основі дорівнюють 38° і 52^o. Знайдіть довжину відрізка, який з'єднує середини основ, довжини яких 18 см і 12 см.

4. Три менші сторони рівнобічної трапеції рівні між собою. В якому відношенні діагональ трапеції поділяє висоту, проведену з вершини тупого кута, якщо діагоналі точкою перетину діляться у відношенні 3 : 7.

5. Діагоналі рівнобічної трапеції є бісектрисами її тупих кутів і в точці перетину діляться у відношенні 3:13. Обчисліть периметр трапеції, якщо її висота дорівнює 48 см.

6. Діагональ рівнобічної трапеції є бісектрисою гострого кута і ділить висоту, проведену з вершини тупого кута, на відрізки 75 см і 21 см. Обчисліть радіус кола, описаного навколо трапеції.

7. Три сторони трапеції рівні. Коло, побудоване на більшій із основ трапеції, як на діаметрі, ділить бічну сторону пополам. Знайдіть кути трапеції.

8. Діагоналі рівнобічної трапеції взаємно перпендикулярні, а її основи дорівнюють 8 см і 18 см. Знайдіть синус гострого кута трапеції.

9. Побудуйте рівнобічну трапецію за двома кутами, на які діагональ поділяє тупий кут, і висотою.

10. У рівнобічній трапеції центр описаного кола лежить на більшій основі. Діагональ і висота трапеції відповідно дорівнюють 40 см і 24 см. Обчисліть радіус описаного кола.

11. Основи трапеції дорівнюють 3 см і 13см. Одна з бічних сторін трапеції поділена на 5 рівних частин і через точки поділу проведено прямі, паралельні основам. Знайдіть довжини відрізків цих прямих, що містяться між бічними сторонами трапеції.

12. У рівнобедрену трапецію вписано коло. Бічна сторона трапеції поділена точкою дотику на відрізки 1 см і 4 см. Знайдіть радіуси кіл — вписаного у трапецію і описаного навколо неї.

13. Кути при основі трапеції дорівнюють 30° і 60°. Знайдіть діагональ трапеції, проведену з вершини більшого гострого кута трапеції, якщо її основи дорівнюють 10 см і 34 см.

14. Відстань між серединами діагоналей прямокутної трапеції дорівнює 3 см. Знайдіть більшу бічну сторону трапеції, якщо її більший кут дорівнює 120°.

15. У рівнобічній трапеції, діагоналі якої взаємно перпендикулярні, довжини основ дорівнюють 6 см та 14 см. Знайдіть периметр чотирикутника, вершини якого є серединами сторін трапеції.

16. Діагональ рівнобічної трапеції перпендикулярні, а висота трапеції дорівнює 5 см. Знайти площу трапеції.

17. Діагональ рівнобічної трапеції є бісектрисою гострого кута і ділить висоту, проведену з вершини тупого куга, у відношенні 5 : 2. Знайдіть середню лінію трапеції, якщо її периметр дорівнює 96 см.

Задачі на розв’язування трапеції

1. Діагональ рівнобічної трапеції є бісектрисою гострого кута і ділить висоту , проведену з вершини тупого кута, на відрізки 75 см і 21 см. Знайти периметр трапеції.

2. Діагональ прямокутної трапеції ділить тупий кут пополам, а другу діагональ — у відношенні 2:5. Обчислити периметр трапеції , якщо її висота дорівнює 24 см.

3. Діагоналі рівнобічної трапеції є бісектрисами гострих кутів і в точці перетину діляться у відношенні 11:5. Обчислити периметр

трапеції, якщо її висота дорівнює 24 см.

4. Діагоналі рівнобічної трапеції є бісектрисами тупих кутів і в точці перетину діляться у відношенні 11:25. Обчислити периметр трапеції, якщо її висота дорівнює 24 см.

5. Основи рівнобічної трапеції дорівнюють 50 см і 14 см, а діагональ дорівнює 40 см. Обчислити площу трапеції.

6. Основа і більша діагональ прямокутної трапеції відповідно дорівнюють 7, 16 і 20 см. Знайти бічні сторони трапеції.

7. Основи трапеції дорівнюють 6 см і 16 см. Одна з бічних сторін дорівнює 10 см і утворює з більшою основою кут 60 град. Знайти діагоналі трапеції.

8. Основи рівнобічної трапеції дорівнюють 25 см і 7 см, а діагональ перпендикулярна до бічної сторони. Знайти бічну сторону трапеції.

9. Основи трапеції дорівнюють 8 і 42 см, а діагоналі - 30 і 40 см. Обчислити площу трапеції.

10.Основи трапеції дорівнюють 28 і 11 см, а бічні сторони - 25 і 26 см. Знайти висоту трапеції.

11.Перпендикуляр, опущений з вершини тупого кута рівнобічної трапеції на більшу основу, ділить її на відрізки 25 см і 7 см. Знайти радіус вписаного кола.

12.Бісектриси гострих кутів при основі трапеції перетинаються на другій основі і дорівнюють 13 см і 15 см. Обчислити периметр трапеції, якщо її висота дорівнює 12 см.

13.Бічна сторона, висота й діагональ рівнобічної трапеції відносяться, як 13:12:20. Знайти основи трапеції, якщо її середня лінія дорівнює 32 см.

14.Бічні сторони і висота трапеції відповідно дорівнюють 25, 30 і 24 см. Бісектриси тупих кутів при основі трапеції перетинаються на другій її основі. Знайти периметр трапеції.

15.Більша діагональ прямокутної трапеції є бісектрисою прямого кута. Різниця основ дорівнює 16 см, а різниця бічних сторін - 4 см. Обчислити периметр трапеції.

16.В рівнобічній трапеції більша основа дорівнює 44 см, бічна сторона 17 см і діагональ 39 см. Знайти площу трапеції.

17.Точки дотику вписаного у трапецію кола ділять бічну сторону на відрізки 9 см і 16 с, а другу бічну сторону - на відрізки, різниця яких дорівнює 10 см. Знайти основи трапеції.

18.Точки дотику вписаного у трапецію кола ділять одну бічну сторону на відрізки 9 см і 16 см, а другу - на відрізки у відношенні 4:9. Знайти основи трапеції.

19.Центр описаного навколо рівнобічної трапеції кола лежить на більшій основі. Бічна сторона і висота трапеції відповідно дорівнюють 30 см і 24 см. Знайти радіус описаного кола

20.Центр кола, вписаного в прямокутну трапецію , віддалений від кінців бічної сторони на 2 см і 4 см. Знайти площу трапеції.

21.Менша основа і бічна сторона трапеції утворюють кут 120 град, і відповідно дорівнюють 15 см і 10 см. Сума основ трапеції дорівнює 46 см. Знайти другу бічну сторону трапеції.

22.Менша діагональ прямокутної трапеції, довжина якої 15 см, є бісектрисою прямого кута. Обчислити периметр трапеції, якщо різниця її основ дорівнює 9 см.

23.У рівнобічній трапеції центр описаного кола лежить на більшій основі. Діагональ і висота трапеції відповідно дорівнюють 40 і 24 см. Знайти радіус описаного кола.

24.Сума основ прямокутної трапеції дорівнює 23 см, а різниця бічних сторін - 3 см. Обчислити периметр трапеції, якщо більша діагональ дорівнює 20 см.

25.Різниця основ прямокутної трапеції дорівнює 9 см, а сума бічних сторін - 27 см. Обчислити периметр трапеції , якщо менша діагональ трапеції дорівнює 20 см.

26. Бісектриси тупих кутів при основі трапеції перетинаються на другій основі, а бічні сторони дорівнюють 13 і 15см. Знайдіть основи трапеції, якщо її висота дорівнює 12см.

27. Бісектриса тупого кута прямокутної трапеції ділить більшу основу на відрізки 5 і 15см. Обчисліть периметр трапеції, якщо її висота дорівнює 11см.

28. Більша діагональ прямокутної трапеції є бісектрисою прямого кута. Різниця основ трапеції дорівнює 30см, а різниця бічних сторін - 10см. Обчисліть площу трапеції.

29. Периметр рівнобічної трапеції дорівнює 100см, а менша основа -18см. Знайди радіус вписаного кола.

30. Центр, вписаного у прямокутну трапецію кола, віддалений від кінців меншої основи на 12 см і 15см, починаючи від вершини прямокутного кута. Знайти сторони трапеції.

31. Діагональ рівнобічної трапеції перпендикулярна до бічної сторони. Знайдіть діагональ трапеції, якщо її основи дорівнюють 25 і 7см.

32. У рівнобічній трапеції з гострим кутом 60° і периметром 144см діагональ ділить середню лінію на відрізки, різниці між якими дорівнює 16 см. Знайдіть основи трапеції.

33. Кінці більшої сторони прямокутної трапеції віддалені від центра вписаного у неї кола на 15 і 20см. Обчисліть периметр трапеції.

34. Середня лінія трапеції дорівнює 10см. і ділить площу трапеції у відношенні 3:5. Знайти основи трапеції.

35. Менша діагональ прямокутної трапеції ділить середню лінію на відрізки 5 і 11см. Обчисліть периметр трапеції, якщо її висота дорівнює 9см.

36. Бічна сторона трапеції дорівнює 10см. і утворює з більшою основою, довжина якої 22см., кут 60°. Сума основ трапеції дорівнює 28см. Знайдіть другу бічну сторону трапеції.

37. Основи прямокутної трапеції дорівнюють 25 і 32см., а більша діагональ є бісектрисою гострого кута. Обчисліть периметр трапеції.

38. У рівнобічній трапеції центр вписаного кола лежить на більшій основі. Висота і різниця основ трапеції відповідно дорівнюють 24 і 36см. Обчисліть радіус описаного кола.

39. Основи прямокутної трапеції дорівнюють 21 і 28см. Обчисліть радіус вписаного у неї кола.

40. Бічні сторони трапеції дорівнюють 25 і 30см., а висота - 24см. Бісектриси гострих кутів при основі трапеції перетинаються на другій основі. Обчисліть площу трапеції.

41. Бічні сторони і висота трапеції відповідно дорівнюють 25, 30 і 24см. Бісектриси гострих кутів при основі трапеції перетинаються на другій основі. Обчисліть периметр трапеції.

42. Основи трапеції дорівнюють 3 і 14см., а діагоналі - 25 і 26см.

Знайдіть висоту трапеції.

43. Довжини основ рівнобічної трапеції відносяться, як 5:12, а висота її дорівнює 17см. Знайти радіус кола, описаного навколо трапеції, якщо відомо, що середня лінія трапеції дорівнює висоті.

44. Центр описаного навколо рівнобічної трапеції кола лежить на більшій основі. Менша основа трапеції дорівнює 14см., а висота -24см. Обчислити радіус описаного кола.

45. У рівнобічній трапеції з тупим кутом 120° і периметром 220см. діагональ ділить середню лінію у відношенні 5:6. Знайдіть бічні сторони трапеції.

46. Діагональ рівнобічної трапеції дорівнює 10см., а площа дорівнює 48см2. Знайти висоту трапеції.

47РВисота рівнобічної трапеції дорівнює 14см., а основи - 16 і 12см. Знайти площу описаного кола.

48. Діагональ рівнобічної трапеції є бісектрисою гострого кута і ділить середню лінію на відрізки 13 і 23см. Знайдіть висоту трапеції.

49. Більша діагональ прямокутної трапеції є бісектрисою гострого кута. Сума основ трапеції дорівнює 31см., а сума бічних сторін -25см. Знайдіть основи та висоту трапеції.

50. Діагональ рівнобічної трапеції з основами 25 і 39см є бісектрисою гострого кута. Знайдіть висоту трапеції.

51. Основи рівнобічної трапеції дорівнюють 13 і 37см., а діагоналі взаємно перпендикулярні. Обчисліть площу трапеції.

52. Бісектриса гострого кута ділить меншу основу прямокутної трапеції на відрізки 5 і 15 см. Обчисліть периметр трапеції, якщо її більша основа дорівнює 29 см.

53. В рівнобічній трапеції довжина середньої лінії дорівнює 5, а діагоналі взаємно перпендикулярні. Знайти площу трапеції.

54.Бісектриси гострих кутів при основі трапеції перетинаються на другій основі, а бічні сторони дорівнюють 13 і 15 см. Знайдіть основи трапеції, якщо її висота дорівнює 12 см.

55.Основи прямокутної трапеції дорівнюють 25 і 37 см, а менша діагональ є бісектрисою тупого кута. Обчисліть периметр трапеції.

56. Діагональ рівнобічної трапеції з основами 7 і 25 см перпендикулярна до бічної сторони. Знайдіть цю діагональ.

57. В рівнобічній трапеції довжина висоти дорівнює 4, а діагоналі взаємно перпендикулярні. Знайти площу трапеції.

58. В рівнобічній трапеції відстані від точки перетину діагоналей до основ дорівнюють 3 см та 4 см. Бічна сторона дорівнює 25 см. Знайти довжину відрізка, який проходить через діагоналі та паралельний основам трапеції. Знайти площу трапеції.

59. В прямокутну трапецію вписано коло. Більша бічна сторона трапеції ділиться точкою дотику на відрізки, що дорівнюють 4 см та 9 см. Знайти площу трапеції та невідомі сторони трапеції.

60. У прямокутній трапеції менша діагональ дорівнює 25 см, менша основа дорівнює 15 см. Знайти площу та невідомі сторони трапеції, якщо менша діагональ перпендикулярна до більшої бічної сторони.