Банк задач з теми «Трапеція»





Банк задач з теми «Трапеція»
Картинки по запросу класифікація трапецій Картинки по запросу класифікація трапеційКартинки по запросу властивості трапецій

Картинки по запросу властивості трапецій

1. Діагональ рівнобічної трапеції є бісектрисою гострого кута і ділить висоту , проведену з вершини тупого кута, на відрізки 75 см і 21 см. Знайти периметр трапеції.
2. Діагональ прямокутної трапеції ділить тупий кут пополам, а другу діагональ — у відношенні 2:5. Обчислити периметр трапеції , якщо її висота дорівнює 24 см.
3. Діагоналі рівнобічної трапеції є бісектрисами гострих кутів і в точці перетину діляться у відношенні 11:5. Обчислити периметр
трапеції, якщо її висота дорівнює 24 см.
4. Діагоналі рівнобічної трапеції є бісектрисами тупих кутів і в точці перетину діляться у відношенні 11:25. Обчислити периметр трапеції, якщо її висота дорівнює 24 см.
5. Основи рівнобічної трапеції дорівнюють 50 см і 14 см, а діагональ дорівнює 40 см. Обчислити площу трапеції.
6. Основа і більша діагональ прямокутної трапеції відповідно дорівнюють 7, 16 і 20 см. Знайти бічні сторони трапеції.
7. Основи трапеції дорівнюють 6 см і 16 см. Одна з бічних сторін дорівнює 10 см і утворює з більшою основою кут 60 град. Знайти діагоналі трапеції.
8. Основи рівнобічної трапеції дорівнюють 25 см І 7 см, а діагональ  перпендикулярна до бічної сторони. Знайти бічну сторону трапеції.
9.  Основи трапеції дорівнюють 8 і 42 см, а діагоналі - 30 і 40 см. Обчислити площу трапеції.
10.Основи трапеції дорівнюють 28 і 11 см, а бічні сторони - 25 і 26 см. Знайти висоту трапеції.
11.Перпендикуляр, опущений з вершини тупого кута рівнобічної трапеції на більшу основу, ділить її на відрізки 25 см і 7 см. Знайти радіус вписаного кола.
12.Бісектриси гострих кутів при основі трапеції перетинаються на другій основі і дорівнюють 13 см і 15 см. Обчислити периметр трапеції, якщо її висота дорівнює 12 см.
13.Бічна сторона, висота й діагональ рівнобічної трапеції відносяться, як 13:12:20. Знайти основи трапеції, якщо її середня лінія дорівнює 32 см.
14.Бічні сторони і висота трапеції відповідно дорівнюють 25, 30 і 24 см. Бісектриси тупих кутів при основі трапеції перетинаються на другій її основі. Знайти периметр трапеції.
15.Більша діагональ прямокутної трапеції є бісектрисою прямого кута. Різниця основ дорівнює 16 см, а різниця бічних сторін - 4 см. Обчислити периметр трапеції.
16.В рівнобічній трапеції більша основа дорівнює 44 см, бічна сторона 17 см і діагональ 39 см. Знайти площу трапеції.
17.Точки дотику вписаного у трапецію кола ділять бічну сторону на відрізки 9 см і 16 с, а другу бічну сторону - на відрізки, різниця яких дорівнює 10 см. Знайти основи трапеції.
18.Точки дотику вписаного у трапецію кола ділять одну бічну сторону на відрізки 9 см і 16 см, а другу - на відрізки у відношенні 4:9. Знайти основи трапеції.
19.Центр описаного навколо рівнобічної трапеції кола лежить на більшій основі. Бічна сторона і висота трапеції відповідно дорівнюють 30 см і 24 см. Знайти радіус описаного кола
20.Центр кола, вписаного в прямокутну трапецію , віддалений від кінців бічної сторони на 2 см і 4 см. Знайти площу трапеції.
21.Менша основа і бічна сторона трапеції утворюють кут 120 град, і відповідно дорівнюють 15 см і 10 см. Сума основ трапеції дорівнює 46 см. Знайти другу бічну сторону трапеції.
22.Менша діагональ прямокутної трапеції, довжина якої 15 см, є бісектрисою прямого кута. Обчислити периметр трапеції, якщо різниця її основ дорівнює 9 см.
23.У рівнобічній трапеції центр описаного кола лежить на більшій основі. Діагональ і висота трапеції відповідно дорівнюють 40 і 24 см. Знайти радіус описаного кола.
24.Сума основ прямокутної трапеції дорівнює 23 см, а різниця бічних сторін - 3 см. Обчислити периметр трапеції, якщо більша діагональ дорівнює 20 см.
25.Різниця основ прямокутної трапеції дорівнює 9 см, а сума бічних сторін - 27 см. Обчислити периметр трапеції , якщо менша діагональ трапеції дорівнює 20 см.
26. Бісектриси тупих кутів при основі трапеції перетинаються на
другій основі, а бічні сторони дорівнюють 13 і 15см. Знайдіть основи трапеції, якщо її висота дорівнює 12см.
27. Бісектриса тупого кута прямокутної трапеції ділить більшу основу на відрізки 5 і 15см. Обчисліть периметр трапеції, якщо її висота дорівнює 11см.
28. Більша діагональ прямокутної трапеції є бісектрисою прямого кута. Різниця основ трапеції дорівнює 30см, а різниця бічних сторін - 10см. Обчисліть площу трапеції.
29. Периметр рівнобічної трапеції дорівнює 100см, а менша основа -18см. Знайди радіус вписаного кола.
30. Центр, вписаного у прямокутну трапецію кола, віддалений від кінців меншої основи на 12 см і 15см, починаючи від вершини прямокутного кута. Знайти сторони трапеції.
31. Діагональ    рівнобічної   трапеції   перпендикулярна   до    бічної сторони. Знайдіть діагональ трапеції, якщо її основи дорівнюють 25  і  7см.
32. У рівнобічній трапеції з гострим кутом 60° і периметром 144см діагональ ділить середню лінію на відрізки, різниці між якими дорівнює 16 см. Знайдіть основи трапеції.
33. Кінці більшої сторони прямокутної трапеції віддалені від центра вписаного у неї кола на 15 і 20см. Обчисліть периметр трапеції.
34. Середня лінія трапеції дорівнює 10см. і ділить площу трапеції у відношенні 3:5. Знайти основи трапеції.
35. Менша діагональ прямокутної трапеції ділить середню лінію на відрізки 5 і 11см. Обчисліть периметр трапеції, якщо її висота дорівнює 9см.
36. Бічна сторона трапеції дорівнює 10см. і утворює з більшою основою, довжина якої 22см., кут 60°. Сума основ трапеції дорівнює 28см. Знайдіть другу бічну сторону трапеції.
37. Основи прямокутної трапеції дорівнюють 25 і 32см., а більша діагональ є бісектрисою гострого кута. Обчисліть периметр трапеції.
38. У рівнобічній трапеції центр вписаного кола лежить на більшій основі. Висота і різниця основ трапеції відповідно дорівнюють 24 і 36см. Обчисліть радіус описаного кола.
39. Основи прямокутної трапеції дорівнюють 21 і 28см. Обчисліть радіус вписаного у неї кола.
40. Бічні сторони трапеції дорівнюють 25 і 30см., а висота - 24см. Бісектриси гострих кутів при основі трапеції перетинаються на другій основі. Обчисліть площу трапеції.
41. Бічні сторони і висота трапеції відповідно дорівнюють 25, 30 і 24см. Бісектриси гострих кутів при основі трапеції перетинаються на другій основі. Обчисліть периметр трапеції.
42. Основи трапеції дорівнюють 3 і 14см., а діагоналі - 25 і 26см.
Знайдіть висоту трапеції.
43. Довжини основ рівнобічної трапеції відносяться, як 5:12, а висота її дорівнює 17см. Знайти радіус кола, описаного навколо трапеції, якщо відомо, що середня лінія трапеції дорівнює висоті.
44. Центр описаного навколо рівнобічної трапеції кола лежить на більшій основі. Менша основа трапеції дорівнює 14см., а висота -24см. Обчислити радіус описаного кола.
45. У рівнобічній трапеції з тупим кутом 120° і периметром 220см. діагональ ділить середню лінію у відношенні 5:6. Знайдіть бічні сторони трапеції.
46. Діагональ рівнобічної трапеції дорівнює 10см., а площа дорівнює 48см2. Знайти висоту трапеції.
47РВисота рівнобічної трапеції дорівнює 14см., а основи - 16 і 12см. Знайти площу описаного кола.
48. Діагональ рівнобічної трапеції є бісектрисою гострого кута і ділить середню лінію на відрізки 13 і 23см. Знайдіть висоту трапеції.
49. Більша діагональ прямокутної трапеції є бісектрисою гострого кута. Сума основ трапеції дорівнює 31см., а сума бічних сторін -25см. Знайдіть основи та висоту трапеції.
50. Діагональ   рівнобічної   трапеції   з   основами    25  і 39см є бісектрисою гострого кута. Знайдіть висоту трапеції.
51. Основи рівнобічної трапеції дорівнюють 13 і 37см., а діагоналі взаємно перпендикулярні. Обчисліть площу трапеції.
52. Бісектриса гострого кута ділить меншу основу прямокутної трапеції на відрізки 5 і 15 см. Обчисліть периметр трапеції, якщо її більша основа дорівнює 29 см.
53. В рівнобічній трапеції довжина середньої лінії дорівнює 5, а діагоналі взаємно перпендикулярні. Знайти площу трапеції.
54.Бісектриси гострих кутів при основі трапеції перетинаються на другій основі, а бічні сторони дорівнюють 13 і 15 см. Знайдіть основи трапеції, якщо її висота дорівнює 12 см.
55.Основи прямокутної трапеції дорівнюють 25 і 37 см, а менша діагональ є бісектрисою тупого кута. Обчисліть периметр трапеції.
56. Діагональ рівнобічної трапеції з основами 7 і 25 см перпендикулярна до бічної сторони. Знайдіть цю діагональ.
Означення.
 Рівнобічна трапеція — це трапеція, у якої бокові сторони рівні.
На цій сторінці представлені формули, що характерні рівнобічній трапеції. Не забувайте, що для рівнобічної трапеції виконуються всі формули та властивості трапеції.
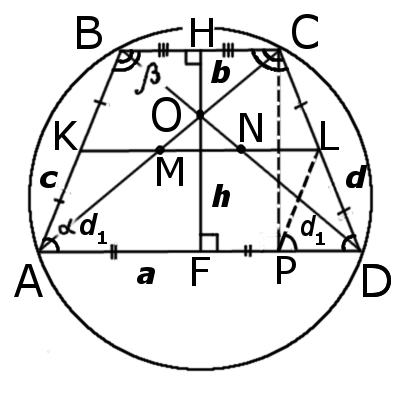Зображення рівнобічної трапеції з позначеннями
Рис.1

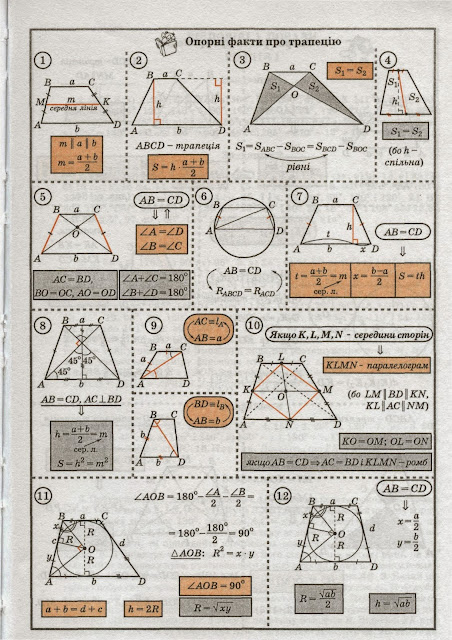
Ознаки рівнобічної трапеції

Трапеція буде рівнобічною, якщо виконується одна із цих умов:
1. Кути при основі рівні:
∠ABC = ∠BCD і ∠BAD = ∠ADC
2. Діагоналі рівні:
AC = BD
3. Однакові кути між діагоналями і основами:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сума протилежних кутів дорівнює 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
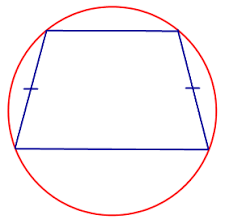
5. Навколо трапеції можна описати коло

Основні властивості рівнобічної трапеції

1. Сума кутів прилеглих до бокової сторони рівнобічної трапеції дорівнює 180°:
∠ABC + ∠BAD = 180° і ∠ADC + ∠BCD = 180°
2. Якщо в рівнобічну трапецію можна вписати коло, то бокова сторона дорівнює середній лінії трапеції:
AB = CD = m
3. Навколо рівнобічної трапеції можна описати коло
4. Якщо діагоналі взаємно перпендикулярні, то висота дорівнює півсумі основ (середній лінії):
h = m
5. Якщо діагоналі взаємно перпендикулярні, то площа трапеції дорівнює квадрату висоти:
SABCD = h2
6. Якщо в рівнобічну трапецію можна вписати коло, то квадрат висоти рівний добутку основ трапеції:
h2 = BC · AD
7. Сума квадратів діагоналей дорівнює сумі квадратів бокових сторін плюс подвоєному добутку основ трапеції:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8. Пряма, що проходить через середини основ, перпендикулярна основам і являється віссю симетрії трапеції:
HF ┴ BC ┴ AD
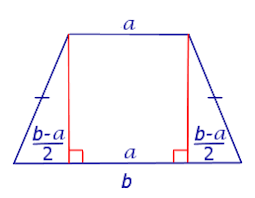
9. Висота (CP), опущена із вершини (C) на більшу основу (AD), ділить її на більший відрізок (AP), який дорівнює півсумі основ та менший (PD) - дорівнює піврізниці основ:
AP = BC + AD
2
PD = AD - BC
2

Сторони рівнобічної трапеції

Формули довжин сторін рівнобічної трапеції:

1. Формули довжин сторін через інші сторони, висоту та кут:
a = b + 2h ctg α = b + 2c cos α
b = a - 2h ctg α = a - 2c cos α
c = h = a - b
sin α2 cos α
2. Формула довжини сторін трапеції через діагоналі та інші сторони:
a = d12 - c2       b = d12 - c2       c = √d12 - ab
ba
3. Формули довжини основ через площу, висоту та іншу основу:
a = 2S- b      b = 2S- a
hh
4. Формули довжини бокової сторони через площу, середню лінію та кут при основі:
с = S
m sin α
5. Формули довжини бокової сторони через площу, основи та кут при основі:
с = 2S
(a + b) sin α

Середня лінія рівнобічної трапеції

Формули довжини середньої лінії рівнобічної трапеції:

1. Формула визначення довжини середньої лінії через основи, висоту та кут при основі:
m = a - h ctg α = b + h ctg α = a - √c2 - h2 = b + √c2 - h2
2. Формула середньої лінії трапеції через площу та сторону:
m = S
c sin α

Висота рівнобічної трапеції

Формули визначення довжини висоти рівнобічної трапеції:

1. Формула висоти через сторони:
h = 1√4c2 - (a - b)2
2
2. Формула висоти через сторони та кут прилеглий до основи:
h = a - btg β = c sin β
2

Діагоналі рівнобічної трапеції

Діагоналі рівнобічної трапеції рівні:
d1 = d2

Формула довжини діагоналей рівнобічної трапеції:

1. Формула довжини діагоналі через сторони:
d1 = √с2 + ab
2. Формули довжини діагоналі по теоремі косинусів:
d1 = √a2 + c2 - 2ac cos α
d1 = √b2 + c2 - 2bc cos β
3. Формула довжини діагоналі через висоту та середню лінію:
d1 = √h2 + m2
4. Формула довжини діагоналі через висоту та основи:
d1 = 1√4h2 + (a + b)2
2

Площа рівнобічної трапеції

Формули площі рівнобічної трапеції:

1. Формула площі через сторони:
S = a + b√4c2 - (a - b)2
4
2. Формула площі через сторони та кут:

S = (b + c cos α) c sin α = (a - c cos α) c sin α
3. Формула площі через радіус вписаного кола та кут між основою та боковою стороною:
S = 4 r 2 = 4 r 2
sin αsin β
4. Формула площі через основи та кут між основою та боковою стороною:
S = ab = ab
sin αsin β
5. Формула площі рівнобічної трапеції, в яку можна вписати коло:

S = (a + b) · r = √ab·c = √ab·m
6. Формула площі через діагоналі та кут між ними:
S = d12· sin γ = d12· sin δ
22
7. Формула площі через середню лінію, бокову сторону та кут при основі:

S = mc sin α = mc sin β
8. Формула площі через основи та висоту:
S = a + b· h
2

Коло описане навколо трапеції

Коло можна описати лише навколо рівнобічної трапеції!!!

Формула радіуса описаного навколо трапеції кола:

1. Формула радіуса через сторони та діагональ:

R = a·c·d1
4√p(p - a)(p - c)(p - d1)
де
p = a + c + d1
2
a - більша основа


Коментарі

Дописати коментар

Популярні дописи з цього блогу

Властивості трапеції

Зображення
"Найбільша помилка - вважати, що ти ніколи не помиляєшся." Томас Карлейль Трапеція                                     Трапе́ція  — це чотирикутник, дві протилежні сторони якого  паралельні . Паралельні сторони називаються  основами  трапеції (сторони AB та DC на малюнку). Інші сторони називаються  бічними сторонами  (сторони AD та CB). Виділяють три спеціальні класи трапецій: ·           Рівнобічна  трапеція, тобто трапеція у якої бічні сторони рівні. ·           Прямокутна  трапеція — це трапеція у якої два кута прямі. ·           Різностороння  трапеція, у якої всі сторони різні. Відрізок,...
Докладніше

Контрольна робота з теми «Подібність трикутників»

Контрольна робота з теми «Подібність трикутників» Варіант 1. Початковий та середній рівень. У завданнях 1-6 виберіть правильну відповідь. 1.(1 бал) Сторони D АВС а = 3 м, b = 4 м, c = 5 м . Знайдіть найменшу сторону подібного йому D А 1 В 1 С 1 , якщо найбільша сторона с 1 = 2,5 м. А) 6 м;    Б) 2 м;       В) 1,5 м;      Г) 2,5 м;       Д) інша відповідь. 2. (1 бал) Точки М та Р лежать відповідно на сторонах  АВ та СВ D АВС, причому РМ çç АС. Знайдіть сторону  ВС, якщо АС =12  м, МР = 4 м, ВР = 5 м . А)15 м;    Б) 10 м;       В) 12 м;      Г) 18 м;       Д) інша відповідь. 3. (1 бал) Відрізки АВ та МР перетинаються в точці О, АО:ОВ = РО:ОМ = 2:3,  ВМ=15 м. Знайдіть довжину відрізка АР. А)18 м;    Б) 22,5 м;   ...
Докладніше

Властивості прямокутних трикутників

Довідник з геометрії прямокутного трикутника Властивості  прямокутних трикутників 1. У прямокутному трикутнику сума гострих кутів рівна 90 0 . 2. Рівнобедрений прямокутний трикутник має рівні гострі кути по 45 0 . 3. У прямокутному трикутнику напроти кута 30 0 лежить катет, що дорівнює половині гіпотенузи. 4. Площа прямокутного трикутника рівна половині добутку  його катетів. 5. У прямокутному трикутнику медіана, що проведена до гіпотенузи рівна половині гіпотенузи. 6. У прямокутному трикутнику кут між бісектрисами гострих кутів рівний 135 0 . 7. У прямокутному трикутнику бісектриса прямого кута ділить кут між медіаною та висотою, що проведені з вершини прямого кута навпіл. 8. У прямокутному трикутнику висота, що проведена з прямого кута розділяє трикутник його на два прямокутних трикутники, у яких рівні кути. 9. У прямокутному трикутнику медіана, що проведена з прямого кута розділяє трикутник його на два необов’язково рівних рівнобедрених трикутн...
Докладніше