Формули площі трикутника

Формули площі трикутника

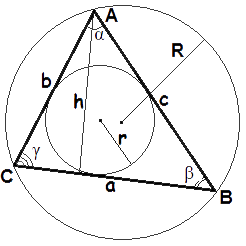
1. Формула площі трикутника за стороною та висотою
   Площа трикутника дорівнює половині добутку довжини сторони трикутника та довжини проведеної до цієї сторони висоти
   

   S =	1	a · h
   	2

2. Формула площі трикутника за трьома сторонами
   

   Формула Герона

   S = √p(p - a)(p - b)(p - c)
3. Формула площі трикутника за двома сторонами і кутом між ними
   Площа трикутника дорівнює половині добутку двох його сторін помноженого на синус кута між ними.
   

   S =	1	a · b · sin γ
   	2

4. Формула площі трикутника за трьома сторонам і радіусом описаного кола
   

   S =	a · b · с
   	4R

5. Формула площі трикутника за трьома сторонами і радіусом вписаного кола
   Площа трикутника дорівнює добутку півпериметра трикутника на радіус вписаного кола.
   

   S = p · r

   
   де S - площа трикутника,
   a, b, c - довжини сторін трикутника,
   h - висота трикутника,
   γ - кут між сторонами a и b,
   r - радіус вписаного кола,
   R - радіус описаного кола,
   

   p =	a + b + c	- півпериметр трикутника.
   	2

   
   

Задачі з теми «Площа трикутника»

1.Найбільша сторона АВ  трикутника АВС  і найменша висота СН, що проведена до цієї сторони, рівні між собою і  дорівнюють по 8 см.

Знайти:

а) площу трикутника  АВС;    

б) площу новоутвореного трикутника РМК, сторони якого являються середніми  лініями трикутника АВС;

в) площу новоутвореного трикутника ЕОН, якщо він має вдвічі більшу сторону, ніж сторона  АВ трикутника АВС, і вдвічі меншу висоту, ніж висота СН трикутника АВС;

г)довжини усіх cторін правильного трикутника XYZ, якщо площі трикутників  XYZ та АВС рівні;

д) усі висоти правильного трикутника XYZ, якщо площа трикутника  XYZ вдвічі більша, ніж площа трикутника АВС;

е) найменшу висоту прямокутного рівнобедреного трикутника KLM, якщо площа трикутників  KLM та АВС рівні;

2. Найбільша сторона АВ  трикутника АВС  і найменша висота СН, що проведена до цієї сторони, рівні між собою і  дорівнюють по 12 см.

Довести, що:

а) АВС – не являється рівностороннім трикутником;

б) АВС – не являється рівнобедреним прямокутним трикутником;

в) АВС – може виявиться гострокутним рівнобедреним трикутником;

г) АВС – може виявиться тупокутним рівнобедреним трикутником;

 3. Площа трикутника АВС дорівнює 72 см².

Знайти:

а) сторону АВ, якщо висота СН, що проведена до неї, дорівнює 18 см.

б) кут трикутника АСВ, якщо СВ =9 см,  СА=16 см;

в) периметр трикутника АВС, якщо радіус вписаного кола  в цей трикутник дорівнює 36 см;

г) висоту СН трикутника АВС, якщо сторона АВ=24 см;

д) радіус вписаного  кола в трикутник АВС, якщо периметр трикутника дорівнює 72 см;

е) добуток трьох сторін трикутника АВС, якщо радіус описаного кола дорівнює 2 см.

є) сторону АН, якщо трикутник АВС – правильний.

ж) сторону АВ, якщо трикутник АВС – правильний.

з) сторону АВ, якщо трикутник АВС – прямокутний рівнобедрений.

и) сторону АВ, якщо трикутник АВС – правильний.

і) найменшу висоту, якщо трикутник АВС – прямокутний рівнобедрений.

4. У прямокутного трикутника АВС, катет  СВ =8 см, а гіпотенуза АВ=17 см. 

Знайти:

а) площу трикутника АВС;

б) найменшу висоту трикутника АВС;

в) площу трикутника АСН, якщо СН – висота трикутника АВС;

г) площу трикутника ВСН, якщо СН – висота трикутника;

д) радіус вписаного кола в трикутник АВС;

е) площу трикутника СВМ, якщо ВМ – медіана трикутника АВС;

є) площу трикутника АСК, якщо АК – медіана трикутника АВС;

ж) площу трикутника РСК, якщо СК – медіана трикутника АВС, СР – бісектриса трикутника АВС.

5. Накреслити три різні трикутники, які мають рівні площі. Чи обов’язково у цих трикутників  є рівні елементи?

6.Знайти площу трикутника, дві сторони якого 9 см і 3 см, а кут між ними дорівнює: 1) 45; 2) 150.

7. Дві сторони трикутника дорівнюють 7 см і 6 см. Чи може його площа дорівнювати:  1) 23 см²; 2) 21 см²;

3) 17 см².

8. Основа першого трикутника 6 см, а основа другого – 9 см. Яким повинно бути відношення висот першого та другого трикутників, щоб площа другого трикутника була у 2 рази більша за площу першого?

9. Знайти площу рівнобедреного трикутника, бічна сторона якого дорівнює  17 см, а висота, проведена до основи, - 5 см.

10. Катет прямокутного трикутника дорівнює 10 см, а гіпотенуза – 26 см. Знайти висоту трикутника, проведену до гіпотенузи.

11. Як зміниться площа трикутника, якщо:

1) його основу збільшити у 8 разів;

2) його висоту зменшити у  5 разів;

3) основу збільшити у    12 разів, а висоту зменшити у 4 рази;

4)  основу зменшити у 9 разів, а висоту – у 7 разів?

12. Як зміниться площа трикутника, якщо:

1) його основу збільшити у 12 разів;

2) його висоту зменшити у  4 разів;

3) основу збільшити у   8 разів, а висоту зменшити у 2 рази;

4)  основу зменшити у 7 разів, а висоту – у 7 разів?

Заповнити таблицю "ТРИКУТНИКИ"

№	a	b	c	α	β	γ	S	hc	ha	hb	mc	mb	ma	lc	lb	la	R	r
№	a	b	c	α	β	γ	S	hc	ha	hb	mc	mb	ma	lc	lb	la	R	r
1		1	3	60o
2	2		5		30o
3		3	9			45o
4	4		6		135o
5		5	4	150o
6		6	8			120o
7	7	5		60o
8	8		6		30o
9	9	8				45o
10		9	7		135o
11	7	4		150o
12		4	5			120o
13		1	3	60o
14	2		5		30o
15		3	9			45o
16	4		6		135o
17		7	5	150o
18		8	9			120o
19	7	6		60o
20	8		7		30o
21	5	8				45o
22		9	7		135o
23	8	4		150o
25		5	6			120o
26		4	3	60o
27	9		5		30o
28		3	7			45o
29	8		6		135o
30		3	4	150o
31		4	8			120o
32	9	5		60o
33	5		4		30o
34	3	2				45o
35		4	2		135o
36	9	4		150o
37		2	6			120o
38		2	5	60o
39	6		5		30o

Заповнити таблицю "ПРЯМОКУТНІ ТРИКУТНИКИ"

Прямокутний

3-кутник:

a,b,c- сторони трикутника,

ά, β,γ - кути трикутника,

h_a, h_b, h _c - висоти трикутника,

m_a, m_b, m_c - медіани трикутника,

l_a, l_b, l_c - бісектриси трикутника ,S - площа трикутника,

R - радіус описаного кола,

r - радіус вписаного кола,

а_с - проекція катета а на сторону с ,

b_c – проекція катета b на сторону с_.

№	a	b	c	S	p	hc	mc	mb	ma	lc	lb	la	R	r	α	β
1	3	4
2		12	13
3	6		10
4		24	25
5	8		17
6		12	15
7		40	41
8	10	24
9	11		61
10	12	16
11		35	37
12	13	84
13		48	50
14	15		25
15	15		39
16		30	34
17	16	63
18		24	30
19	18	80
20	20		29
21		48	52
22	21		35