ТЕОРЕМА ПІФАГОРА

Теорема звучить так:

У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах.

Позначивши довжину гіпотенузи трикутника як c, а довжини катетів як a та b, отримаємо такі формули:

${\displaystyle a^{2}+b^{2}=c^{2}.\,}$

${\displaystyle {\sqrt {a^{2}+b^{2}}}=c.\,}$

Таким чином, теорема Піфагора встановлює співвідношення, яке дозволяє визначити сторону прямокутного трикутника, знаючи довжини двох інших. Відповідно, в алгебраїчній інтерпретації теорему можна сформулювати так:

У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи.

Теорема Піфагора є окремим випадком теореми косинусів, котра визначає співвідношення між сторонами довільного трикутника.

Також доведено зворотне твердження (називають також зворотною до теореми Піфагора):

Для будь-яких трьох додатних чисел a, b і c, для яких виконується рівняння a² + b² = c², існує прямокутний трикутник з катетами a та b і гіпотенузою c.

Використання подібних трикутників.

Самостійна робота  з теми  "ТЕОРЕМА   ПІФАГОРА"

Варіант І

1. Сторони прямокутного трикутника 9см, 12см і 15 см. Знайти синуси, косинуси і тангенси гострих кутів.

2. Знайти гіпотенузу прямокутного трикутника, якщо його катети 6 і 8 см.

3. Дві сторони трикутника 5 см і 10 см. Яким найбільшим і яким найменшим цілим числом сантиметрів може виражатись третя сторона даного трикутника?

4. Розв'язати прямокутний трикутник, гострий кут якого 30°, а протилежний до нього катет 5 см.

5. У прямокутному трикутнику гострий кут а, протилежний до даного кута катет а. Знайти висоту даного трикутника, опущену на гіпотенузу.

Варіант 2

1. Сторони прямокутного трикутника 10 см, 24см і 26см. Знайти синуси, косинуси і тангенси гострих кутів.

2. Знайти катет прямокутного трикутника, якщо другий його катет 12 см, а гіпотенуза 15 см.

3. Діагоналі паралелограма 18 см і 10 см. Яким найбільшим і яким найменшим цілим числом сантиметрів може виражатись сторона даного паралелограма?

4. Розв'язати прямокутний трикутник, гострий кут якого 60°, а протилежний до нього катет 4 см.

5. Знайти висоту прямокутного трикутника, опущену на гіпотенузу, якщо катет даного трикутника а, величина гострого кута, прилеглого до даного катета а.

Варіант 3

1. Сторони прямокутного трикутника 8 см, 15 см і 17 см. Знайти синуси, косинуси і тангенси гострих кутів.

2. Знайти катет прямокутного трикутника, якщо другий його катет 30 см, а гіпотенуза 34 см.

3. Сторона ромба 6 см. Яким найбільшим і яким найменшим цілим числом сантиметрів може виражатись діагональ даного ромба?

4. Розв'язати прямокутний трикутник, в якому гострий кут 30°, а гіпотенуза 10 см.

5. У прямокутному трикутнику висота, яка проведена до гіпотенузи дорівнює а, кут між даною висотою та катетом а. Знайти гіпотенузу даного трикутника.

Варіант 4

1. Сторони прямокутного трикутника 14 м, 48 м, 50 м. Знайти синуси, косинуси і тангенси гострих кутів.

2. У рівнобедреному прямокутному трикутнику гіпотенуза 10 см. Знайти катети даного трикутника.

3. Діагональ прямокутника 12 см. Яким найбільшим і яким найменшим цілим числом сантиметрів може виражатись сторона даного прямокутника?

4. Розв'язати прямокутний трикутник, в якому гострий кут 60°, а гіпотенуза 20 см.

5. Знайти висоту прямокутного трикутника, яка проведена до гіпотенузи, якщо кут між висотою та катетом р, а гіпотенуза даного трикутника с.

Піфагорові трійки

Докладніше: Піфагорові трійки    a² + b² = c², 

Піфагорові трійки — це три натуральні числа a, b, та c такі, що виконується рівність a² + b² = c². Іншими словами, Піфагорові трійки — це сторони прямокутного трикутника, якщо всі вони є цілими. На мегалітичних спорудах в північній Європі є свідчення, що відомості про такі трійки були відомі до винайдення писемності. Такі трійки зазвичай записують у вигляді (a, b, c). Деякі найвідоміші приклади: (3, 4, 5) та (5, 12, 13).

Примітивними Піфагоровими числами називають такі a, b та c, які є взаємно простими (найбільший спільний дільник a, b та c дорівнює 1)

Нижче наведено перелік примітивних Піфагорових чисел менших за 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97).

Найкраще запам'ятовуються такі Піфагорові числа (менші за 100):

(3, 4, 5), (6, 8, 10), (9, 12, 15), (12, 16, 20), (15, 20, 25), (18, 24, 30), (21, 28, 35), (24, 32, 40), (27, 36, 45), (30, 40, 50), (33, 44, 55), (36, 48, 60), (39, 52, 65), (42, 56, 70), (45, 60, 75), (48, 64, 80), (51, 68, 85), (54, 72, 90), (57, 76, 95), (60, 80, 100).

Ці трійки утворюються множенням першої трійки чисел (3, 4, 5) на числа 2, 3, 4, 5 тощо.

Узагальнення

Подібні геометричні фігури на трьох сторонах

Узагальнення для подібних трикутників, площа зелених фігур A + B = площі синіх C

Теорема Піфагора з використанням подібних прямокутних трикутників

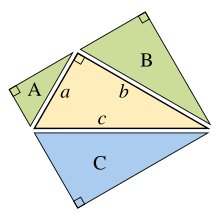
Узагальнення теореми Піфагора робив Евклід в своїй праці Начала, розширивши площі квадратів на сторонах до площ подібних геометричних фігур:^[14]

Якщо побудувати подібні геометричні фігури (див. Евклідова геометрія) на сторонах прямокутного трикутника, тоді сума двох менших фігур буде дорівнювати площі більшої фігури.

Головна ідея цього узагальнення полягає в тому, що площа подібної геометричної фігури пропорційна до квадрату будь-якого свого лінійного розміру і зокрема до квадрату довжини будь-якої сторони. Отже, для подібних фігур з площами A, B і C, що побудовані на сторонах з довжиною a, b і c, маємо:

${\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,,}$

${\displaystyle \Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C\,.}$

Але, за теоремою Піфагора, a² + b² = c², тоді A + B = C.

І навпаки, якщо ми зможемо довести, що A + B = C для трьох подібних геометричних фігур без використання теореми Піфагора, тоді ми зможемо довести саму теорему, рухаючись у зворотному напрямку. Наприклад, стартовий центральний трикутник може бути повторно використаний як трикутник C на гіпотенузі, і два подібні прямокутні трикутники (A і B), побудовані на двох інших сторонах, які утворюються в результаті поділу центрального трикутника його висотою. Сума площ двох менших трикутників тоді очевидно дорівнює площі третього, таким чином A + B = C і, виконуючи попереднє доведення в зворотному порядку, отримаємо теорему Піфагора a² + b² = c².

Теорема косинусів

Докладніше: Теорема косинусів

Теорема Піфагора — це окремий випадок загальнішої теореми косинусів, яка пов'язує довжини сторін в довільному трикутнику:^[15]

${\displaystyle a^{2}+b^{2}-2ab\cos {\theta }=c^{2},\,}$

де θ — кут між сторонами a і b.

Якщо θ дорівнює 90 градусів, тоді cosθ = 0 і формула спрощується до звичайної теореми Піфагора.