Нерівність трикутника

Нерівність трикутника є теоремою в Евклідовій геометрії, доведення присутнє ще в «Началах» Евкліда.

В трикутнику ${\displaystyle \ \Delta ABC:\;\;|AC|\leqslant |AB|+|BC|,}$

 причому рівність ${\displaystyle \ |AC|=|AB|+|BC|}$ досягається тільки тоді, 

коли трикутник вироджений і точка ${\displaystyle B}$ лежить строго між ${\displaystyle A}$ та ${\displaystyle C}$.

Теорема. Довжина сторони трикутника мен­ша від суми двох інших його сторін.

Доведення. Аксіома друга третьої групи стверджує, що для будь-яких трьох точок А, В і С справджується рівність АВ+ВС=АС тоді і тільки тоді, коли точка 5 лежить між точками А і С, тобто  коли усі три точки лежать на  прямій, оскільки найкоротша  відстань між точками А і С  по прямій. Жодна з вершин  трикутника не може лежати між двома іншими, оскільки  тоді не буде трикутника. Тому

АВ+ВС> АС,

або

АС< АВ+ ВС,

що й треба було довести.  

Позначивши   довжини   сторін   трикутника малими буквами, доведені співвідношення  запишемо  у  вигляді:   а<b+с,   b<.а+с, c<a+b

Віднявши від обох частин кожної із записаних нерівностей по відповідній величині, від чого, як відомо, нерівність не порушується, дістанемо нові не­рівності:

b - с< a,

с-a<b і

а - b<с.

Вони ствер­джують, що кожна сторона трикутника більша від різниці двох інших сторін трикутника.

Завдання для індивідуальної роботи.

1. Довжина однієї сторони трикутника 8 см, дру­гої — 5 см.

 Чи може третя сторона цього трикутника мати довжину:

 1) 2 см; 2) 5 см; 3) 8 см; 4) 13 cм; 5) 12 см; 6) 3 см; 7) 12,99 cм; 8) 3,1 см?

Обчислити периметри висоти, бісектриси, медіани існуючих трикут­ників.

2. Чи можна утворити трикутник з трьох відрізків, дов­жини яких становлять: 

1) 1,4 м, 2,6 м і 4 м; 2) 2,5 м, 2,5м і 4м; 3) 1,2м, 1,2м і 2,5м; 

4) 1,23м, 1,35м і 2,57 м? 

Обчислити периметри висоти, бісектриси, медіани існуючих трикут­ників.

Часткові випадки

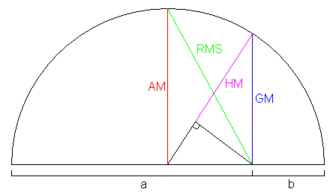
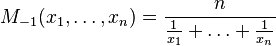   — середнє гармонійне (HM),

   — середнє геометричне (GM),

   — середнє арифметичне (AM),

   — середнє квадратичне (RMS).

Нерівність для медіан трикутника

Будь-яка медіана 
трикутника АВС  

менше півсуми сторін, 
між якими вона лежить:

0,5(a+b-c)<m_c<0,5(b+c)

0,5(a+c-b)<m_b<0,5(a+c)

0,5(b+c-a)<m_a<0,5(a+c)