Площа чотирикутника

Формули площі опуклого чотирикутника

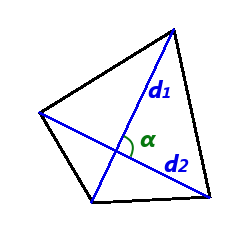
1. Формула площі чотирикутника за довжинами діагоналей і куту між ними
   Площа опуклого чотирикутника дорівнює половині добутку йог діагоналей помноженому на синус кута між ними:
   
   

   S =	1	d1 d2 sin α
   	2

   
   де S - площа чотирикутника,
   d₁, d₂ - довжини діагоналей чотирикутника,
   α - кут між діагоналями чотирикутника.
   
2. Формула площі описаного чотирикутника (за довжиною периметру і радіусу вписаного кола)
   Площа опуклого чотирикутника дорівнює добутку його півпериметру на радіус вписаного кола
   
   
   S = p · r
3. 
   Формула площі чотирикутника за довжиною сторін і значенням протилежних кутів
   
   
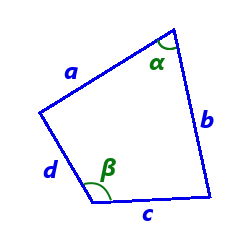   S = √(p - a)(p - b)(p - c)(p - d) - abcd cos²θ
   
   де S - площа чотирикутника,
   a, b, c, d - довжини сторін чотирикутника,
   

   p =	a + b + c + d	- півпериметр чотирикутника,
   	2

   θ =	α + β	- півсума двох протилежних кутів чотирикутника.
   	2

4. Формула площі чотирикутника, навколо якого можна описати коло
   
   
   S = √(p - a)(p - b)(p - c)(p - d)

Формули площі квадрата

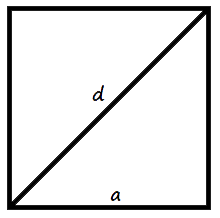
1. Формула площі квадрата за довжиною сторони
   Площа квадрата дорівнює квадрату довжини його сторони.
   
   
   S = a²
2. Формула площі квадрата за довжиною діагоналі
   Площа квадрата дорівнює половині квадрата довжини його діагоналі.
   

   S =	1	d2
   	2

   
   де S - Площа квадрата,
   a - довжина сторін квадрата,
   d - довжина діагоналей квадрата.

Ви можете використати онлайн калькулятор для розрахунку площі квадрата.

Формула площі прямокутника

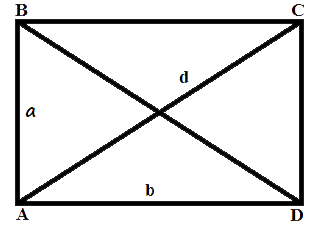
Площа прямокутника дорівнює добутку довжин двох його суміжних сторін

S = a · b

де S - площа прямокутника,
a, b - довжини сторін прямокутника.

Ви можете використати онлайн калькулятор для розрахунку площі прямокутника.

Формули площі паралелограма

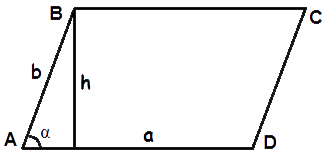
1. Формула площі паралелограма за довжиною сторони і висоти
   Площа паралелограма дорівнює добутку довжин його сторони і опущеної на цю сторону висоти.
   
   
   S = a · h
2. Формула площі паралелограма за двома сторонами і кутом між ними
   Площа паралелограма дорівнює добутку довжин його сторін помноженому на синус кута між ними.
   
   S = a · b · sin α
3. Формула площі паралелограма за двома діагоналями і кутом між ними
   Площа паралелограма дорівнює половині добутку довжин його діагоналей, помноженого на синус кута між ними.
   

   S =	1	d1d2 sin γ
   	2

   
   де S - площа паралелограма,
   a, b - довжини сторін паралелограма,
   h - довжина висоти паралелограма,
   d₁, d₂ - довжини діагоналей паралелограма,
   α - кут між сторонами паралелограма,
   γ - кут між діагоналями паралелограма.

Ви можете використати онлайн калькулятор для розрахунку площі паралелограма.

Формули площі ромба

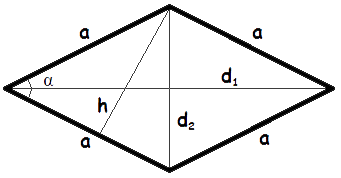
1. Формула площі ромба за довжиною сторони і висоти
   Площа ромба дорівнює добутку довжин його сторони і опущеної на цю сторону висоти.
   
   
   S = a · h
2. Формула площі ромба за довжиною сторони і кутом
   Площа ромба дорівнює добутку квадрату довжини його сторони і синуса кута між сторонами ромба.
   
   S = a² · sin α
3. Формула площі ромба за довжинами його діагоналей
   Площа ромба дорівнює половині добутку довжин його діагоналей.
   
   

   S =	1	d1 · d2
   	2

   
   де S - площа ромба,
   a - довжина сторони ромба,
   h - довжина висоти ромба,
   α - кут між сторонами ромба,
   d₁, d₂ - довжини діагоналей.

Ви можете використати онлайн калькулятор для розрахунку площі ромба.

Формула площі трапеції

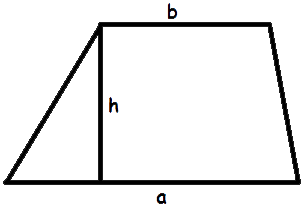
1. Формула Герона для трапеції
   
   

   S =	a + b	√(p - a)(p - b)(p - a - c)(p - a - d)
   	|a - b|

2. Формула площі трапеції за довжиною основ і висоти
   Площа трапеції дорівнює добутку півсуми її основ та висоти
   

   S =	1	(a + b) · h
   	2

   де S - площа трапеції,
   a, b - довжини основ трапеції,
   c, d - довжини бокових сторін трапеції,
   

   p =	a + b + c + d	- півпериметр трапеції.
   	2

Задачі на трапеціях

1.      Основи трапеції 10 см і 15 см, а діагоналі — 7 см і 24 см. Знайдіть висоту трапеції.

2.      Діагоналі рівнобічної трапеції діляться точкою перетину у відношенні 1 :4. Знайдіть периметр трапеції, якщо його бічна сторона і висота до­рівнюють відповідно 20 см і 16 см.

3.      Два кути трапеції при одній основі дорівнюють 38° і 52^o. Знайдіть довжи­ну відрізка, який з'єднує середини основ, довжини яких 18 см і 12 см.

4.      Три менші сторони рівнобічної трапеції рівні між собою. В якому відношенні діагональ трапеції поділяє висоту, проведену з вершини тупого кута, якщо діагоналі точкою перетину діляться у відношенні 3 : 7.

5.      Діагоналі рівнобічної трапеції є бісектрисами її тупих кутів і в точці перетину діляться у відношенні 3:13. Обчисліть периметр трапеції, якщо її висота дорівнює 48 см.

6.      Діагональ рівнобічної трапеції є бісектрисою гострого кута і ділить висоту, проведену з вершини тупого кута, на відрізки 75 см і 21 см. Об­числіть радіус кола, описаного навколо трапеції.

7.      Три сторони трапеції рівні. Коло, побудоване на більшій із основ трапе­ції, як на діаметрі, ділить бічну сторону пополам. Знайдіть кути трапеції.

8.      Діагоналі рівнобічної трапеції взаємно  перпендикулярні, а її основи дорівнюють 8 см і 18 см. Знайдіть синус гострого кута трапеції.

9.      Побудуйте рівнобічну трапецію за двома кутами, на які діагональ поділяє тупий кут, і висотою.

10.  У рівнобічній трапеції центр описаного кола лежить на більшій ос­нові. Діагональ і висота трапеції відповідно дорівнюють 40 см і 24 см. Обчисліть радіус описаного кола.

11.  Основи трапеції дорівнюють 3 см і 13см. Одна з бічних сторін трапеції поділена на 5 рівних частин і через точки поділу проведено прямі, па­ралельні  основам.   Знайдіть довжини   відрізків   цих   прямих,   що містяться між бічними сторонами трапеції.

12.  У рівнобедрену трапецію вписано коло. Бічна сторона трапеції поділена точкою дотику на відрізки 1 см і 4 см. Знайдіть радіуси кіл — вписаного у трапецію і описаного навколо неї.

13.  Кути при основі трапеції дорівнюють 30° і 60°. Знайдіть діагональ тра­пеції, проведену з вершини більшого гострого кута трапеції, якщо її основи дорівнюють 10 см і 34 см.

14.  Відстань між серединами діагоналей прямокутної трапеції дорівнює 3 см. Знайдіть більшу бічну сторону трапеції, якщо її більший кут дорівнює 120°.

15.  У рівнобічній трапеції, діагоналі якої взаємно перпендикулярні, довжини основ дорівнюють 6 см та 14 см. Знайдіть периметр чотирикут­ника, вершини якого є серединами сторін трапеції.

16.  Діагональ рівнобічної трапеції перпендикулярні, а висота трапеції дорівнює 5 см. Знайти площу трапеції.

17.  Діагональ рівнобічної трапеції є бісектрисою гострого кута і ділить висоту, проведену з вершини тупого куга, у відношенні 5 : 2. Знайдіть середню лінію трапеції, якщо її периметр дорівнює 96 см.