Подібні трикутники в прямокутному трикутнику і крузі

Подібні трикутники


               
Визначення: Два трикутники називаються подібними, якщо сторони одного трикутника відповідно пропорційні сторонам  другого та їхні відповідні кути рівні.
Число, яке рівне відношенню відповідних сторін подібних трикутників називають коефіцієнтом подібності.
Для подібності двох трикутників використовують символ₪.

Рівні трикутники подібні, у них коефіцієнт подібності рівний 1.
Ознаки подібності трикутників

Ознака 1.Два трикутники подібні, якщо два кути одного трикутника відповідно рівні двом кутам другого трикутника.
Ознака 2. Два трикутники подібні, якщо дві сторони одного трикутника відповідно пропорційні двом сторонам другого трикутника і кути між цими сторонами рівні.
Ознака 3. Два трикутники подібні, якщо три сторони одного трикутника відповідно пропорційні двом сторонам другого трикутника

Властивості подібних трикутників
1. Два трикутники подібні, якщо сторони одного відповідно паралельні сторонам другого.
2. Два трикутники подібні, якщо сторони одного відповідно перпендикулярні сторонам другого.
3. У рівносторонні трикутники  подібні.
4. Пряма, що паралельна стороні трикутника і перетинає дві інші сторони цього трикутника відтинає від нього трикутник, що подібний до даного.
5. Площі двох подібних трикутників відносяться, як квадрати  відповідних лінійних елементів.

6. Гомотетичні трикутники подібні.

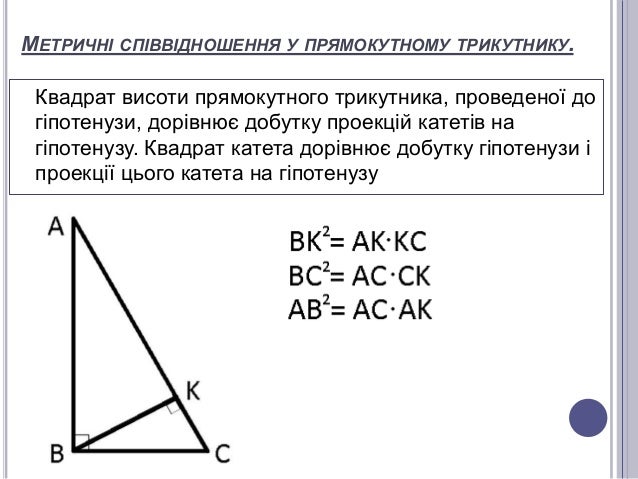
Результат пошуку зображень за запитом "подібні трикутники"

ПРОПОРЦІЙНІ ВІДРІЗКИ 
В ПРЯМОКУТНОМУ ТРИКУТНИКУ

 Результат пошуку зображень за запитом "подібні трикутники"


1. Знайти висоту прямокутного трикутника, проведену з вершини прямого кута, якщо вона ділить гіпотенузу на відрізки довжиною 4 см і 16 см.
2. Катет прямокутного трикутника дорівнює 8 см, а його проекція на гіпотенузу – 4 см. Знайти гіпотенузу.
3. Висота прямокутного трикутника, проведена до гіпотенузи , ділить її на відрізки довжиною 18 см і 32 см. Знайти катети трикутника.
4. Один катет прямокутного трикутника дорівнює 4 см, а проекція другого катета на гіпотенузу – 6 см. Знайти другий катет та гіпотенузу.
5. Катети прямокутного трикутника дорівнюють 9 см і 12 см. Знайти висоту трикутника, проведену з вершини прямого кута.
6. У прямокутного DАВС(ÐС = 90о, ÐВ= 60о) виразити через відношення сторін такі тригонометричні  величини: 
sin ÐВ =?,  sin ÐA=?,  cos ÐВ=? ,  cosÐA=?,  tgÐВ=? ,  tgÐA=? ,  ctgÐВ=? , ctgÐA=?
7. Використовуючи трійку сторін (а; b; с) прямокутного DАВС(ÐС = 90о) знайти  числові значення тригонометричних виразів:   sinÐВ =?,  sinÐA=?,  cos ÐВ=? ,  cosÐA=?,  tgÐВ=? ,  tgÐA=? ,  ctgÐВ=? , ctgÐA=?   якщо:  1)( 9; 40; 41);  2) (189; 340; 380);  3) (21; 20; 29);  4) (7; 24; 25) ;  5) (45; 28; 53);  6) (21; 220; 221);  7) (13; 84; 85);  8) (65; 72; 97);  9)( 69; 260; 269); 10) (165; 52; 173);  11) (57; 176; 185);  12) (88; 105; 137); 13) (77; 36; 85);   14) (45; 28; 53);   15) (33; 56; 65);   16) (11, 60, 61).  
8. Використовуючи трійку сторін (а; b; с) прямокутного DАВС(ÐС = 90о) знайти числові значення тригонометричних виразів:   sin ÐВ =?,  sin ÐA=?,  cos ÐВ=? ,  cosÐA=?,  tgÐВ=? ,  tgÐA=? ,  ctgÐВ=? , ctgÐA=?   якщо є тільки  дві відомі сторони: 1)( 15; 8; с);  2) (35; 12; с);  3) (а; 12; 13);  4) (а; 24; 25);  5) (45; b; 53);  6) (33; b; 65);  7) (а; 84; 85);  8) (63; 16; с);  9)(а; 112; 113); 10) (165; b; 173);  11) (а; 260; 269);  12) (312; b; 313).   
9. Виписати тільки правильні твердження для прямокутного DАВС(ÐС = 90о,  СН -висота):
1)   sin ÐВ = СА/AB; 
2)   sin ÐA=CB/AB;
3)   cos ÐВ= CB/AB;
4)   cosÐA = СА/AB;  
5)   tgÐВ =CA/CB; 
6)   tgÐA  = CB/AC;
7)   ctgÐВ = CB/AC; 
8)   сtgÐA = CA/CB; 
9)   sin ÐВ = СН/ВС; 
10)        sin ÐA=CН/AС;
11)        cos ÐВ = НB/СB;
12)       cosÐA = НА/AС;
13)        tgÐВ =CН/НB;
14)        tgÐA  = CН/AН;
15)       ctgÐВ = НB/НC;  
16)        ctgÐA = НA/CН.
10. Знайти катет АС прямокутного DАВС(ÐС = 90о, ÐВ= 60о) з гіпотенузою, що рівна:  1) 8м;  2) 12 см;  3) 4 км;   4) 24 см;   5) 44м;  6) 33 см;  7) 84 см;  8) 16 см;  9) 11 см;  10) 13 см; 11) 26 см; 12) b см.   
11. Знайти катет ВС прямокутного DАВС(ÐС = 90о, ÐВ= 30о) з гіпотенузою, що рівна:  1) 8м;   2) 10 см;  3)1 км;   4) 26 см;     5) 48м;  6) 36 см;  7) 84 см;  8) 16 см;  9) 11 см;  10) 13 см; 11) 26 см; 12) n см.   
12.  Знайти гіпотенузу АВ прямокутного DАВС(ÐС = 90о, ÐВ= 45о) з катетом, що рівний:  1)8м;   2) 12 см;  3)1 км;   4) 24 см;     5) 44м;  6) 33 см;  7) 84 см;  8) 16 см;  9) 11 см;  10) 13 см; 11) 26 см; 12) k см.   
13. Знайти катет ВС прямокутного DАВС(ÐС = 90о, ÐВ= 60о) з катетом АС, що рівний:  1)8м;   2) 12 см;  3)1 км;   4) 24 см;     5) 44м;  6) 33 см;  7) 84 см;  8) 16 см;  9) 11 см;  10) 13 см; 11) 26 см; 12) b см.   




Результат пошуку зображень за запитом "теорема птолемея доказательство"


Результат пошуку зображень за запитом "теорема птолемея доказательство"

Результат пошуку зображень за запитом "теорема птолемея доказательство"

Теорема Птолемея
Четырехугольники вписанные в окружность свойства теорема Птолемея
Четырехугольники вписанные в окружность свойства теорема Птолемея

Результат пошуку зображень за запитом "теорема птолемея доказательство"






Результат пошуку зображень за запитом "теорема птолемея доказательство"



Картинки по запросу властивості хорд що перетинаються
Картинки по запросу властивості хорд що перетинаються
Картинки по запросу властивості хорд що перетинаються
Картинки по запросу властивості хорд що перетинаються




Результат пошуку зображень за запитом "теорема птолемея доказательство"













Теорема Монжа  про спільні дотичні до трьох кіл, що не перетинаються



Коментарі

Дописати коментар

Популярні дописи з цього блогу

Властивості трапеції

Зображення
"Найбільша помилка - вважати, що ти ніколи не помиляєшся." Томас Карлейль Трапеція                                     Трапе́ція  — це чотирикутник, дві протилежні сторони якого  паралельні . Паралельні сторони називаються  основами  трапеції (сторони AB та DC на малюнку). Інші сторони називаються  бічними сторонами  (сторони AD та CB). Виділяють три спеціальні класи трапецій: ·           Рівнобічна  трапеція, тобто трапеція у якої бічні сторони рівні. ·           Прямокутна  трапеція — це трапеція у якої два кута прямі. ·           Різностороння  трапеція, у якої всі сторони різні. Відрізок,...
Докладніше

Контрольна робота з теми «Подібність трикутників»

Контрольна робота з теми «Подібність трикутників» Варіант 1. Початковий та середній рівень. У завданнях 1-6 виберіть правильну відповідь. 1.(1 бал) Сторони D АВС а = 3 м, b = 4 м, c = 5 м . Знайдіть найменшу сторону подібного йому D А 1 В 1 С 1 , якщо найбільша сторона с 1 = 2,5 м. А) 6 м;    Б) 2 м;       В) 1,5 м;      Г) 2,5 м;       Д) інша відповідь. 2. (1 бал) Точки М та Р лежать відповідно на сторонах  АВ та СВ D АВС, причому РМ çç АС. Знайдіть сторону  ВС, якщо АС =12  м, МР = 4 м, ВР = 5 м . А)15 м;    Б) 10 м;       В) 12 м;      Г) 18 м;       Д) інша відповідь. 3. (1 бал) Відрізки АВ та МР перетинаються в точці О, АО:ОВ = РО:ОМ = 2:3,  ВМ=15 м. Знайдіть довжину відрізка АР. А)18 м;    Б) 22,5 м;   ...
Докладніше

Властивості прямокутних трикутників

Довідник з геометрії прямокутного трикутника Властивості  прямокутних трикутників 1. У прямокутному трикутнику сума гострих кутів рівна 90 0 . 2. Рівнобедрений прямокутний трикутник має рівні гострі кути по 45 0 . 3. У прямокутному трикутнику напроти кута 30 0 лежить катет, що дорівнює половині гіпотенузи. 4. Площа прямокутного трикутника рівна половині добутку  його катетів. 5. У прямокутному трикутнику медіана, що проведена до гіпотенузи рівна половині гіпотенузи. 6. У прямокутному трикутнику кут між бісектрисами гострих кутів рівний 135 0 . 7. У прямокутному трикутнику бісектриса прямого кута ділить кут між медіаною та висотою, що проведені з вершини прямого кута навпіл. 8. У прямокутному трикутнику висота, що проведена з прямого кута розділяє трикутник його на два прямокутних трикутники, у яких рівні кути. 9. У прямокутному трикутнику медіана, що проведена з прямого кута розділяє трикутник його на два необов’язково рівних рівнобедрених трикутн...
Докладніше